
题目列表(包括答案和解析)
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
|
|
|
|
|
|
人数 |
4 |
8 |
|
5 |
3 |
表2:
|
生产能力分组 |
|
|
|
|
|
人数 |
6 |
y |
36 |
18 |
(1)先确定 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)

(2)分别估计 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)
(本小题12分)在数学考试中,小明的成绩在90分以上的概率是0.18,在80至89分的概率是0.51,在70至79分的概率是0.15,在60至69分的概率是0.09.计算小明在数学考试中取得80分以上成绩的概率和小明考试及格的概率.
(本小题12分)
已知某商品的价格 (元)与需求量
(元)与需求量 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
|
|
14 |
16 |
18 |
20 |
22 |
|
|
12 |
10 |
7 |
5 |
3 |
(1)画出 关于
关于 的散点图
的散点图
(2)用最小二乘法求出回归直线方程
(3)计算 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 | 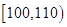 | 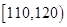 | 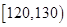 | 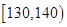 | 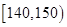 |
| 人数 | 4 | 8 |  | 5 | 3 |
| 生产能力分组 | 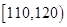 | 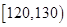 | 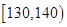 | 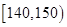 |
| 人数 | 6 | y | 36 | 18 |
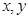 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
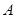 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)(本小题12分)某乡镇为了盘活资本,优化组合,决定引进资本拯救出现严重亏损的企业。长年在外经商的王先生为了回报家乡,决定投资线路板厂和机械加工厂。王先生经过预算,如果引进新技术在优化管理的情况下,线路板厂和机械加工厂可能的最大盈利率分别为95﹪和80﹪,可能的最大亏损率分别为30﹪和10﹪。由于金融危机的影响,王先生决定最多出资100万元引进新技术,要求确保可能的资金亏损不超过18万元.问王先生对线路板厂和机械加工厂各投资多少万元,才能使可能的盈利最大?
一、1 B 2 D
二、13、3 14、-160 15、.files/image211.gif) 16、
16、.files/image213.gif)
三、17、解: (1).files/image215.gif)
.files/image002.gif) ……
3分
……
3分
.files/image217.gif)
.files/image133.gif) 的最小正周期为
的最小正周期为.files/image219.gif)
.files/image002.gif) …………………
5分
…………………
5分
(2) .files/image221.gif) ,
………………… 7分
,
………………… 7分
.files/image223.gif) ………………… 10分
………………… 10分
.files/image217.gif)
.files/image225.gif)
.files/image002.gif) …………………
11分
…………………
11分
.files/image217.gif) 当
当.files/image135.gif) 时,函数
时,函数.files/image133.gif) 的最大值为1,最小值
的最大值为1,最小值.files/image227.gif)
.files/image002.gif) ………… 12分
………… 12分
18、(I)解:设这箱产品被用户拒绝接收事件为A,被接收为.files/image229.gif) ,则由对立事件概率公式
,则由对立事件概率公式
.files/image231.gif) 得:
得:.files/image233.gif)
即这箱产品被用户拒绝接收的概率为.files/image235.gif)
.files/image002.gif) …………
6分
…………
6分
(II).files/image237.gif)
.files/image239.gif) ………… 10分
………… 10分
.files/image241.gif)
1
2
3
P
.files/image243.gif)
.files/image245.gif)
.files/image247.gif)
…………11分
∴ E.files/image241.gif) =
=.files/image250.gif) …………12分
…………12分
19、解法一:
.files/image252.jpg) (Ⅰ)连结B
(Ⅰ)连结B.files/image254.gif) 于O,则O是B
于O,则O是B.files/image254.gif) C的中点,连结DO。
C的中点,连结DO。
∵在△A.files/image257.gif) C中,O、D均为中点,
C中,O、D均为中点,
∴A.files/image257.gif) ∥DO …………………………2分
∥DO …………………………2分
∵A.files/image257.gif)
.files/image259.gif) 平面B
平面B.files/image139.gif) D,DO
D,DO.files/image262.gif) 平面B
平面B.files/image139.gif) D,
D,
∴A.files/image257.gif) ∥平面B
∥平面B.files/image139.gif) D。…………………4分
D。…………………4分
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠.files/image139.gif) DC = 60°,∴C
DC = 60°,∴C.files/image139.gif) =
= .files/image264.gif) 。
。
作DE⊥BC于E。
∵平面BC.files/image139.gif) ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC.files/image139.gif)
.files/image257.gif)
作EF⊥B.files/image139.gif) 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B.files/image139.gif)
∴∠DFE是二面角D-B.files/image139.gif) -C的平面角……………………………………8分
-C的平面角……………………………………8分
在Rt△DEC中,DE=.files/image268.gif)
在Rt△BFE中,EF =
BE?sin.files/image270.gif)
∴在Rt△DEF中,tan∠DFE = .files/image272.gif)
.files/image274.gif) ∴二面角D-B
∴二面角D-B.files/image139.gif) -C的大小为arctan
-C的大小为arctan.files/image277.gif) ………………12分
………………12分
解法二:以AC的中D为原点建立坐标系,如图,
设| AD | = 1∵∠.files/image139.gif) DC =60°∴| C
DC =60°∴| C.files/image139.gif) |
=
|
= .files/image264.gif) 。
。
则A(1,0,0),B(0,.files/image264.gif) ,0),C(-1,0,0),
,0),C(-1,0,0),
.files/image282.gif) (1,0
(1,0.files/image264.gif) ),
),.files/image285.gif) ,
,.files/image287.gif)
(Ⅰ)连结.files/image257.gif) C交B
C交B.files/image290.gif) 于O是
于O是.files/image257.gif) C的中点,连结DO,则
O
C的中点,连结DO,则
O.files/image293.gif) .
. .files/image295.gif) =
=.files/image297.gif)
∵A.files/image257.gif)
.files/image259.gif) 平面B
平面B.files/image290.gif) D,
D,
∴A.files/image257.gif) ∥平面B
∥平面B.files/image290.gif) D.……………………………………………………………4分
D.……………………………………………………………4分
(Ⅱ).files/image303.gif) =(-1,0,
=(-1,0,.files/image264.gif) ),
),.files/image306.gif)
设平面B.files/image290.gif) D的法向量为n = ( x , y , z ),则
D的法向量为n = ( x , y , z ),则.files/image309.gif)
即.files/image311.gif) 则有
则有.files/image313.gif) = 0令z = 1
= 0令z = 1
则n = (.files/image264.gif) ,0,1)…………………………………………………………8分
,0,1)…………………………………………………………8分
设平面BC.files/image139.gif)
.files/image257.gif) 的法向量为m = ( x′
,y′,z′)
的法向量为m = ( x′
,y′,z′)
|