
题目列表(包括答案和解析)
已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为![]() .
.
(1)求p的值;
(2)若直角三角形ABC的三个顶点在抛物线L上,且直角顶点B的横坐标为1,过点A、C分别作抛物线L的切线,两切线相交于点D,直线AC与y轴交于点E,当直线BC的斜率在[3,4]上变化时,直线DE斜率是否存在最大值,若存在,求其最大值和此时直线BC的方程;若不存在,请说明理由.

| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
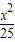 -
-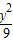 =1与椭圆
=1与椭圆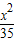 +y2=1有相同的焦点.
+y2=1有相同的焦点.已知抛物线C:![]() ,的焦点为F,经过点F的直线
,的焦点为F,经过点F的直线![]() 交抛物线于A、B两点,过A、B两点分别作抛物线的切线,设两切线的交点为M
交抛物线于A、B两点,过A、B两点分别作抛物线的切线,设两切线的交点为M
(Ⅰ)求点M的轨迹方程;
(Ⅱ)求证MF⊥AB;
(Ⅲ)设△MAB的面积为S,求S的最小值及此时直线![]() 的方程
的方程
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
D
D
C
D
C
C
D
B
C
|