
题目列表(包括答案和解析)
y=2arcsin(2x-1)+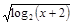 的定义域是( )
的定义域是( )
(A)[ ,1] (B)(0,
,1] (B)(0, )∪(
)∪( ,1]
(C)(
,1]
(C)( ,1] (D)[0,1]
,1] (D)[0,1]
y=2arcsin(2x-1)+ 的定义域是( )
的定义域是( )
A.[ ,1] ,1] | B.(0, )∪( )∪( ,1] ,1] | C.( ,1] ,1] | D.[0,1] |
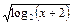 的定义域是( )
的定义域是( )A.[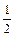 ,1] ,1] | B.(0,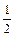 )∪( )∪(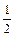 ,1] ,1] | C.(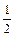 ,1] ,1] | D.[0,1] |
抛物线y=x2+2x-2的顶点坐标是( )
A.(2,-2) B.(1,-2) C.(1,-3) D.(-1,-3)
过抛物线y![]() =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
(A) y![]() =2x-1 (B) y
=2x-1 (B) y![]() =2x-2
=2x-2
(C) y![]() =-2x+1 (D) y
=-2x+1 (D) y![]() =-2x+2
=-2x+2
一.选择题:DBBAC DBDBD
解析:1:由sin x>cos
x>cos x得cos
x得cos x-sin
x-sin x<0, 即cos2x<0,所以:
x<0, 即cos2x<0,所以: +kπ<2x<
+kπ<2x< +kπ,选D.
+kπ,选D.
2:∵复数3- i的一个辐角为-π/6,对应的向量按顺时针方向旋转π/3,
i的一个辐角为-π/6,对应的向量按顺时针方向旋转π/3,
所得向量对应的辐角为-π/2,此时复数应为纯虚数,对照各选择项,选(B)。
3:由 又
又 代入选择支检验
代入选择支检验 被排除;又由
被排除;又由 ,
, 即
即 被排除.故选
被排除.故选 .
.
4:依题意有 , ①
, ①  ②
②
由①2-②×2得, ,解得
,解得 。
。
又由 ,得
,得 ,所以
,所以 不合题意。故选A。
不合题意。故选A。
5:令 ,这两个方程的曲线交点的个数就是原方程实数解的个数.由于直线
,这两个方程的曲线交点的个数就是原方程实数解的个数.由于直线 的斜率为
的斜率为 ,又
,又 所以仅当
所以仅当 时,两图象有交点.由函数
时,两图象有交点.由函数 的周期性,把闭区间
的周期性,把闭区间 分成
分成


 共
共 个区间,在每个区间上,两图象都有两个交点,注意到原点多计一次,故实际交点有
个区间,在每个区间上,两图象都有两个交点,注意到原点多计一次,故实际交点有 个.即原方程有63个实数解.故选
个.即原方程有63个实数解.故选 .
.
6:连接BE、CE则四棱锥E-ABCD的体积VE-ABCD= ×3×3×2=6,又整个几何体大于部分的体积,所求几何体的体积V求> VE-ABCD,选(D)
×3×3×2=6,又整个几何体大于部分的体积,所求几何体的体积V求> VE-ABCD,选(D)
|