练习册

  • 练习册
  • 试题
    (Ⅱ) 求证:ㄓ是钝角三角形; 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数f（x）=aln（1+ex）-（a+1）x，g（x）=x2-（a-1）x-f（lnx），且g（x）在x=1处取得极值．
    （Ⅰ）求实数a的值；
    （Ⅱ）证明：对（-∞，+∞）上任意两个互异的实数x，y，都有f(
    x+y
    2
    )＜
    f(x)+f(y)
    2
    ；
    （Ⅲ）已知△ABC的三个顶点A，B，C都在函数y=f（x）的图象上，且横坐标依次成等差数列，求证△ABC是钝角三角形．并问它可能是等腰三角形吗？说明理由．

    查看答案和解析>>

    已知函数(其中) ,

    点从左到右依次是函数图象上三点,且.

    (Ⅰ) 证明: 函数在上是减函数；

    (Ⅱ) 求证：⊿是钝角三角形;

    (Ⅲ) 试问,⊿能否是等腰三角形?若能,求⊿面积的最大值;若不能,请说明理由．

    查看答案和解析>>

    （本小题满分14分）已知函数.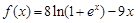

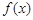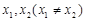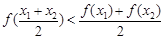    （1）证明：函数 对于定义域内任意都有：成立.

    （2）已知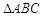的三个顶点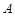、、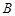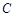都在函数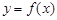的图象上，且横坐标依次成等差数列，求证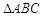：是钝角三角形，但不可能是等腰三角形.

     

    查看答案和解析>>

    对于函数，若存在，使成立，则称为的不动点。如果

    函数有且仅有两个不动点、，且。

    （1）试求函数的单调区间；

    （2）点从左到右依次是函数图象上三点，其中求证：⊿是钝角三角形．

    查看答案和解析>>

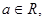    已知函数。

    （1）求函数在区间上最小值；

    （2）对（1）中的，若关于的方程有两个不同的实数解，求实数的取值范围；

    （3）若点A，B，C，从左到右依次是函数图象上三点，且这三点不共线，求证：是钝角三角形。

     

    查看答案和解析>>

    一．选择题：DBBAC DBDBD

    解析：1：由sinx>cosx得cosx－sinx＜0， 即cos2x＜0，所以：＋kπ＜2x＜＋kπ，选D.

     

    2：∵复数3－i的一个辐角为－π/6，对应的向量按顺时针方向旋转π/3，

    所得向量对应的辐角为－π/2，此时复数应为纯虚数，对照各选择项，选（B）。

    3：由又代入选择支检验被排除；又由，即被排除.故选.

    4：依题意有，      ①　　               ②

    由①2-②×2得，，解得。

    又由，得，所以不合题意。故选A。

    5：令，这两个方程的曲线交点的个数就是原方程实数解的个数.由于直线的斜率为，又所以仅当时，两图象有交点.由函数的周期性，把闭区间分成

    共个区间，在每个区间上，两图象都有两个交点，注意到原点多计一次，故实际交点有个.即原方程有63个实数解.故选.

    6：连接BE、CE则四棱锥E－ABCD的体积VE-ABCD=×3×3×2=6，又整个几何体大于部分的体积，所求几何体的体积V求> VE-ABCD，选（D）

    8：在同一直角坐标系中，作出函数

    的图象和直线，它们相交于（－1，1）

    和（1，1）两点，由，得或.

    9：把各选项分别代入条件验算，易知B项满足条件，且的值最小，故选B。

    10：P满足|MP|=|NP|即P是MN的中垂线上的点，P点存在即中垂线与曲线有交点。MN的中垂线方程为2x+y+3=0，与中垂线有交点的曲线才存在点P满足|MP|=|NP|，直线4x+2y-1=0与2x+y+3=0平行，故排除（A）、（C），

    又由△=0，有唯一交点P满足|MP|=|NP|，故选（D）。

    二．填空题：11、； 12、； 13、；14、；15、2；

    解析： 11：由题设，此人猜中某一场的概率为，且猜中每场比赛结果的事件为相互独立事件，故某人全部猜中即获得特等奖的概率为。

    12：分类求和，得

        ，故应填．

    13：依抛物线的对称性可知，大圆的圆心在y轴上，并且圆与抛物线切于抛物线的顶点，从而可设大圆的方程为 

        由  ，消去x，得        （*）

    解出 或

        要使（*）式有且只有一个实数根，只要且只需要即

        再结合半径，故应填

    14.解：直线 化为直角坐标方程是2x+y-1=0; 圆的

    圆心（１，０）到直线2x+y-1=0的距离是

    15.（略）

    三．解答题：

    16、解：（Ⅰ）由, ，

     ．-----------------------6分

    （Ⅱ） 原式＝  

     ．-----------------------12分

     

    17、 (Ⅰ)证明：∵函数是奇函数  ∴

    ∵∴函数不是上的增函数--------------------------------2分

    又函数在上单调  ∴函数为上的单调减函数-------------------4分

       (Ⅱ)由得----------6分

    由(Ⅰ)知函数为上的单调减函数  ∴----------------8分

    即，--------------------------------10分

     ∴原不等式的解集为--------------------------12分

    18、解：(Ⅰ)  

    所以函数在上是单调减函数. …………………………4分

     (Ⅱ) 证明:据题意且x1<x2<x3,

    由(Ⅰ)知f (x1)>f (x2)>f (x3),  x2=…………………………6分

    …………………8分

    即ㄓ是钝角三角形……………………………………..9分

    (Ⅲ)假设ㄓ为等腰三角形，则只能是

     

    即

      ①          …………………………………………..12分

    而事实上,    ②

    由于,故(2)式等号不成立.这与式矛盾.

    所以ㄓ不可能为等腰三角形. ……………………………….14分

    19、解：（Ⅰ）经计算，，，．    …………….2分

    当为奇数时，，即数列的奇数项成等差数列，

    ；  …………………………….4分                   

    当为偶数，，即数列的偶数项成等比数列，

    ．…………………………….6分                            

    因此，数列的通项公式为． ………………………7分

    （Ⅱ），                             

       ……（1）

     …（2）

    （1）、（2）两式相减，

    得     

    ．

       ．……………………………….14分

    20、（I）证明：连结OC

    …………….1分

    ……….2分

    在中，由已知可得

    而

    ……….3分

    即

    平面…………………………….5分

    （II）解：如图建立空间直角坐标系，设平面ACD的法向量为则

          

             …………………….7分

     

           令得是平面ACD的一个法向量。…………………….8分

           又

           点E到平面ACD的距离

           …………………….10分

    （III）     ；

     

      则二面角A-CD-B的余弦值为。…………………………….14分

    21．解 （Ⅰ）由得，                 -----------1分

    当时，，

    此时，，   -----------2分

    ，所以是直线与曲线的一个切点；      -----------3分

    当时，，

    此时，，            -----------4分

    ，所以是直线与曲线的一个切点；       -----------5分

    所以直线l与曲线S相切且至少有两个切点；

    对任意x∈R，，

    所以        ---------------------------------------------------------------------6分

    因此直线是曲线的“上夹线”．        ----------7分

    （Ⅱ）推测：的“上夹线”的方程为       ------9分

    ①先检验直线与曲线相切，且至少有两个切点：设：

     ，

    令，得：（kZ）             ------10分

    当时,

    故：过曲线上的点(，)的切线方程为：

    y－[]= [－()]，化简得：．

    即直线与曲线相切且有无数个切点．    -----12分

    不妨设

    ②下面检验g(x)F(x)

    g(x)－F(x)=

    直线是曲线的“上夹线”．           -----14分


    同步练习册答案