已知某椭圆的焦点是（－4，0），（4，0），过点并垂直于x轴的直线与椭圆的一个交点为B，且|＋｜｜＝10．椭圆上不同的两点A（，），C（，）满足条件：｜A｜，|B｜，|C｜成等差数列．

　　（1）求该椭圆的方程；

　　（2）求弦AC中点的横坐标；

　　（3）设弦AC的垂直平分线的方程为y＝kx＋m，求m的取值范围．

 

查看答案和解析>>

查看答案和解析>>

（本小题满分12分）
已知椭圆C₁和抛物线C₂的焦点均在x轴上，C₁的中心和C₂的顶点均为原点，从它们每条曲线上至少取两个点，将其坐标记录于下表中：   

x	5	－	4
y	2	0	－4		－

（Ⅰ）求C₁和C₂的方程；
（Ⅱ）过点S（0，－）且斜率为k的动直线l交椭圆C₁于A、B两点，在y轴上是否存在定点D，使以线段AB为直径的圆恒过这个点?若存在，求出D的坐标，若不存在，说明理由．

查看答案和解析>>

查看答案和解析>>

（本小题满分12分）.
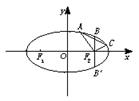
如图，已知某椭圆的焦点是F₁(－4，0)、F₂(4，0)，过点F₂并垂直于x轴的直线与椭圆的一个交点为B，且|F₁B|+|F₂B|=10，椭圆上不同的两点A(x₁,y₁),C(x₂,y₂)满足条件：|F₂A|、|F₂B|、|F₂C|成等差数列.

(1)求该弦椭圆的方程；
(2)求弦AC中点的横坐标；
(3)设弦AC的垂直平分线的方程为y=kx+m，求m的取值范围.

查看答案和解析>>

一、选择题

题号

1

2

3

4

  5

6

7

8

9

10

11

12

答案

B

D

A

D

A

C

A

B

D

C

B

C

二、填空题

13.  ；14.　5　；15. 　；16.  ；17. ①③⑤．

三、解答题（本大题共5题，共.44分，解答题应写出文字说明、演算步骤或证明过程.）

18.解：∵ 椭圆的焦点坐标为（－4，0）和（4，0），……………………2分

则可设双曲线方程为（a＞0，b＞0），

∵ c＝4，又双曲线的离心率等于2，即，∴ a＝2．……………………………4分

∴ ＝12． ………6分；故所求双曲线方程为．　…………8分

19．解：　　 ……………………………………………………2分

……………4分；所以，

由在直线上，故 …………………6分

 ……………………………………………………………8分

20．解：对任意实数都有恒成立；2分

关于的方程有实数根；………………………4分

∨为真命题，∧为假命题，即P真Q假，或P假Q真，……………………5分

如果P真Q假，则有；…………………………………6分

如果P假Q真，则有．………………………………………7分

所以实数的取值范围为． ……………………………………………8分

21. 解：由已知得，点A在x轴上方，设A，

由得，所以A(1，2)，……2分；同理B(4,-4),   …3分

所以直线AB的方程为.……………………………………………4分

设在抛物线AOB这段曲线上任一点，且.

   则点P到直线AB的距离d= …6分

所以当时，d取最大值，………7分；又……………8分

所以△PAB的面积最大值为  ………………………9分

此时P点坐标为.…………………………………………………………10分

22．解：设池底半径为，池高为，成本为，则：

　…………………………………………………………………2分

 …………………4分

　　　　　　　　　　……………………………………………5分

令，得 …………………………………………6分

又时，，是减函数；　……………………………7分

时，，是增函数；　……………………………8分

所以时，的值最小，最小值为……………………9分

答：当池底半径为4米，桶高为6米时，成本最低，最低成本为元.………10分

（三章内容分配：第一章21分，第二章47分，第三章32分）