
题目列表(包括答案和解析)
 (2009•孝感模拟)如图,O(0,0)A(1,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去.有如下结论:
(2009•孝感模拟)如图,O(0,0)A(1,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去.有如下结论:| 1 |
| 2 |
| 63 |
| 64 |
| 21 |
| 64 |
| 3 |
| lim |
| n→∞ |
 的等比数列;
的等比数列;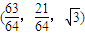 ;
;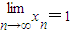 .
.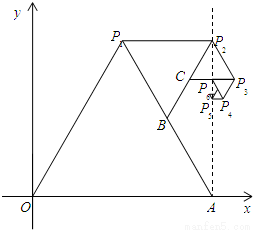
如图,以![]() 、
、![]() 为顶点作正
为顶点作正![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正
为顶点作正![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正
为顶点作正![]() ,…,如此继续下去.有如下结论:
,…,如此继续下去.有如下结论:
①所作的正三角形的边长构成公比为![]() 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线![]() (
(![]() )上;
)上;
③第六个正三角形的不在第五个正三角形边上的顶点![]() 的坐标是
的坐标是![]() ;
;
④第![]() 个正三角形的不在第
个正三角形的不在第![]() 个正三角形边上的顶点
个正三角形边上的顶点![]() 的横坐标是
的横坐标是![]() .
.
其中正确结论的序号是 (把你认为正确结论的序号都填上).

(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2) 若曲线 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线 在变换
在变换 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式![]() :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点![]() 变换到这一平面上的一点
变换到这一平面上的一点![]() .
.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2) 若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换![]() 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com