
题目列表(包括答案和解析)
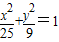 上的一点,O是坐标原点,F是椭圆的左焦点且
上的一点,O是坐标原点,F是椭圆的左焦点且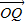 =
= (
(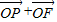 ),|
),|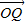 |=4,则点P到该椭圆左准线的距离为( )
|=4,则点P到该椭圆左准线的距离为( )
 上的一点,O是坐标原点,F是椭圆的左焦点且
上的一点,O是坐标原点,F是椭圆的左焦点且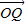 =
= (
(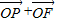 ),|
),| |=4,则点P到该椭圆左准线的距离为( )
|=4,则点P到该椭圆左准线的距离为( )
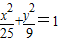 上的一点,O是坐标原点,F是椭圆的左焦点且
上的一点,O是坐标原点,F是椭圆的左焦点且 =
= (
( ),|
),| |=4,则点P到该椭圆左准线的距离为( )
|=4,则点P到该椭圆左准线的距离为( )
已知P是椭圆4x2+y2=1上一点,F为其中一个焦点,则|PF|的最小值为________.
 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线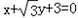 相切.
相切. ,若存在求k的值,若不存在则说明理由.
,若存在求k的值,若不存在则说明理由.
19.解:(1) 平面ABC,AB
平面ABC,AB 平面ABC,∵
平面ABC,∵ AB.
AB.
又 平面
平面 ,且AB
,且AB 平面
平面 ,∴
,∴ 又
又
∴ 平面
平面 .
.
(2) BC∥
BC∥ ,∴
,∴ 或其补角就是异面直线
或其补角就是异面直线 与BC所成的角.
与BC所成的角.
由(1)知 又AC=2,∴AB=BC=
又AC=2,∴AB=BC= ,∴
,∴ .
.
在 中,由余弦定理知cos
中,由余弦定理知cos
∴ =
= ,即异面直线
,即异面直线 与BC所成的角的大小为
与BC所成的角的大小为
 (3)过点D作
(3)过点D作 于E,连接CE,由三垂线定理知
于E,连接CE,由三垂线定理知 ,故
,故
 是二面角
是二面角 的平面角,
的平面角,
又 ,∴E为
,∴E为 的中点,∴
的中点,∴ ,又
,又 ,由
,由
得 ,在Rt
,在Rt CDE中,sin
CDE中,sin ,所以二面角
,所以二面角 正弦值的大小为
正弦值的大小为
20.解:(1)因 ,
, ,故可得直线方程为:
,故可得直线方程为:
(2) ,
, ,用数学归纳法可证.
,用数学归纳法可证.
(3) ,
, ,
, ,
,
所以
21.解:(1)∵
函数 是R上的奇函数 ∴
是R上的奇函数 ∴  即
即 ∴
∴  ,由
,由 的任意性知
的任意性知 ∵
函数
∵
函数 在
在 处有极值,又
处有极值,又
∴  是关于
是关于 的方程
的方程 的根,即
的根,即 ①
①
∵  ∴
∴  ②(4分)由①、②解
②(4分)由①、②解 得
得
(2)由(1)知 ,
,
列表如下:






1
(1,3)
3

+
0
-
0
+


增函数
极大值1
减函数
极小值
增函数
9
∴  在
在 上有最大值9,最小值
上有最大值9,最小值
∵ 任意的 都有
都有 ∴
∴
 ,即
,即
∴  的取值范围是
的取值范围是
22.(1)
(2)由 得
得
 ①
①
设C ,CD中点为M
,CD中点为M ,则有
,则有 ,
, ,
,
 ,又A(0,-1)且
,又A(0,-1)且 ,
, ,
,
即 ,
,
 (此时
(此时 ) ②
) ②
将②代入①得 ,即
,即 或
或 ,
,
综上可得 或
或 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com