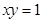求曲线及直线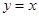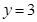，所围成的平面图形的面积.

【解析】本试题主要是考查了定积分的运用。

解：做出曲线xy=1及直线y=x，y=3的草图，则所求面积为阴影部分的面积

解方程组 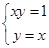得直线y=x与曲线xy=1的交点坐标为（1，1）      

同理得：直线y=x与曲线y=3的交点坐标为（3，3）

        直线y=3与曲线xy=1的交点坐标为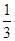（，3）………………3分

因此，所求图形的面积为

 

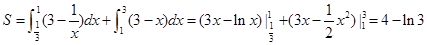
解：因为有负根，所以在y轴左侧有交点，因此

某种产品的广告支出x与销售额y（单位：百万元）之间有如下的对应关系

x	2	4	5	6	8
y	30	40	60	50	70

(1)假定x与y之间具有线性相关关系，求回归直线方程.

（2）若实际销售额不少于60百万元，则广告支出应该不少于多少？

已知函数的图象过坐标原点O,且在点处的切线的斜率是.

（Ⅰ）求实数的值； 

（Ⅱ）求在区间上的最大值；

（Ⅲ）对任意给定的正实数，曲线上是否存在两点P、Q，使得是以O为直角顶点的直角三角形，且此三角形斜边中点在轴上？说明理由.

【解析】第一问当时，，则。

依题意得：，即    解得

第二问当时，，令得，结合导数和函数之间的关系得到单调性的判定，得到极值和最值

第三问假设曲线上存在两点P、Q满足题设要求，则点P、Q只能在轴两侧。

不妨设，则，显然

∵是以O为直角顶点的直角三角形，∴

即    （*）若方程（*）有解，存在满足题设要求的两点P、Q；

若方程（*）无解，不存在满足题设要求的两点P、Q.

（Ⅰ）当时，，则。

依题意得：，即    解得

（Ⅱ）由（Ⅰ）知，

①当时，，令得

当变化时，的变化情况如下表：

		0
	—	0	+	0	—
	单调递减	极小值	单调递增	极大值	单调递减

又，，。∴在上的最大值为2.

②当时, .当时, ,最大值为0；

当时, 在上单调递增。∴在最大值为。

综上，当时，即时，在区间上的最大值为2；

当时，即时，在区间上的最大值为。

（Ⅲ）假设曲线上存在两点P、Q满足题设要求，则点P、Q只能在轴两侧。

不妨设，则，显然

∵是以O为直角顶点的直角三角形，∴

即    （*）若方程（*）有解，存在满足题设要求的两点P、Q；

若方程（*）无解，不存在满足题设要求的两点P、Q.

若，则代入（*）式得：

即，而此方程无解，因此。此时，

代入（*）式得：    即   （**）

令 ，则

∴在上单调递增，  ∵     ∴,∴的取值范围是。

∴对于，方程（**）总有解，即方程（*）总有解。

因此，对任意给定的正实数，曲线上存在两点P、Q，使得是以O为直角顶点的直角三角形，且此三角形斜边中点在轴上

 

5．A解析：因为函数有0，1，2三个零点，可设函数为f(x)=ax(x-1)(x-2)=ax3-3ax2+2ax

因此b=-3a,又因为当x>2时f(x)>0所以a>0,因此b<0

对于回归直线方程，当时，的估计值为　　　　　　　　

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

（2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

已知某地每单位面积的菜地年平均使用氮肥量与每单位面积蔬菜年平均产量之间有的关系如下数据：

年份	x(kg)	y(t)
1985	70	5.1
1986	74	6.0
1987	80	6.8
1988	78	7.8
1989	85	9.0
1990	92	10.2
1991	90	10.0
1992	95	12.0
1993	92	11.5
1994	108	11.0
1995	115	11.8
1996	123	12.2
1997	130	12.5
1998	138	12.8
1999	145	13.0

(1)求x与y之间的相关系数，并检验是否线性相关；

（2）若线性相关，则求蔬菜产量y与使用氮肥x之间的回归直线方程，并估计每单位面积施150kg时，每单位面积蔬菜的平均产量.