
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
已知某地每单位面积的菜地年平均使用氮肥量![]()
![]() 与每单位面积蔬菜年平均产量
与每单位面积蔬菜年平均产量![]() 之间有的关系如下数据:
之间有的关系如下数据:
| 年份 | x(kg) | y(t) |
| 1985 | 70 | 5.1 |
| 1986 | 74 | 6.0 |
| 1987 | 80 | 6.8 |
| 1988 | 78 | 7.8 |
| 1989 | 85 | 9.0 |
| 1990 | 92 | 10.2 |
| 1991 | 90 | 10.0 |
| 1992 | 95 | 12.0 |
| 1993 | 92 | 11.5 |
| 1994 | 108 | 11.0 |
| 1995 | 115 | 11.8 |
| 1996 | 123 | 12.2 |
| 1997 | 130 | 12.5 |
| 1998 | 138 | 12.8 |
| 1999 | 145 | 13.0 |
(1)求x与y之间的相关系数,并检验是否线性相关;
(2)若线性相关,则求蔬菜产量y与使用氮肥x之间的回归直线方程,并估计每单位面积施150kg时,每单位面积蔬菜的平均产量.
见解析
若设![]() ,则
,则![]()
![]()
所以变量![]() 对变量
对变量![]() 的回归方程是
的回归方程是![]()
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
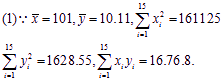 故蔬菜产量与使用氮肥量的相关系数为:
故蔬菜产量与使用氮肥量的相关系数为:
![]()
![]()
由于![]() ,故自由度为15-2=13,由相关系数检验的临界值表查出与显著水平0.05及自由度13相关系数临界值
,故自由度为15-2=13,由相关系数检验的临界值表查出与显著水平0.05及自由度13相关系数临界值![]() 从而可以看出
从而可以看出![]() ,从而说明蔬菜产量与氮肥使用量之间存在相关关系.
,从而说明蔬菜产量与氮肥使用量之间存在相关关系.
(2)设所求的回归直线方程为:![]() ,则
,则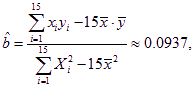
![]()
从而所求的回归直线方程为:![]()
所以当![]() 时,
时,![]()
即估计每单位面积施肥150(t)时,每单位面积蔬菜的年平均产量为![]()


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求导数f′(x);
(2)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;
(3)若f(x)在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
在一次恶劣气候的飞机航程中,调查了男女乘客在飞机上晕机的情况:男乘客晕机的有24人,不晕机的有31人;女乘客晕机的有8人,不晕机的有26人。请你根据所给数据判定是否在恶劣气候飞行中男人比女人更容易晕机?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com