
题目列表(包括答案和解析)
(08年新建二中模拟)如图,过椭圆![]() 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆![]() 的“左特征点”M的坐标;
的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆![]()
![]() 的“左特征点”M是一个怎样的点?并证明你的结论.
的“左特征点”M是一个怎样的点?并证明你的结论.

| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
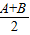 ,β=
,β=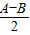
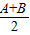 cos
cos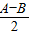 .
.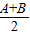 sin
sin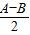 ;
;| X | 1 | 2 | 3 | 4 |
| P | 0.1 | x | 0.3 | 0.1 |
申请某种许可证,根据规定需要通过统一考试才能获得,且考试最多允许考四次. 设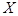 表示一位申请者经过考试的次数,据统计数据分析知
表示一位申请者经过考试的次数,据统计数据分析知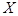 的概率分布如下:
的概率分布如下:
|
|
1 |
2 |
3 |
4 |
|
P |
0.1 |
|
0.3 |
0.1 |
(Ⅰ)求一位申请者所经过的平均考试次数;
(Ⅱ)已知每名申请者参加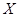 次考试需缴纳费用
次考试需缴纳费用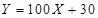 (单位:元),求两位申请者所需费用的和小于500元的概率;
(单位:元),求两位申请者所需费用的和小于500元的概率;
(Ⅲ)在(Ⅱ)的条件下, 4位申请者中获得许可证的考试费用低于300元的人数记为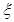 ,求
,求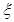 的分布列.
的分布列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com