
题目列表(包括答案和解析)
(本小题满分12分)
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列![]() 中的
中的![]() 、
、![]() 、
、![]() 。
。
(I) 求数列![]() 的通项公式;
的通项公式;
(II) 数列![]() 的前n项和为
的前n项和为![]() ,求证:数列
,求证:数列![]() 是等比数列。
是等比数列。
已知函数
(I) 讨论f(x)的单调性;
(II) 设f(x)有两个极值点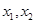 若过两点
若过两点 的直线I与x轴的交点在曲线
的直线I与x轴的交点在曲线 上,求α的值。
上,求α的值。
【解析】本试题考查了导数在研究函数中的运用。第一就是三次函数,通过求解导数,求解单调区间。另外就是运用极值的概念,求解参数值的运用。
【点评】试题分为两问,题面比较简单,给出的函数比较常规,,这一点对于同学们来说没有难度但是解决的关键还是要看导数的符号的实质不变,求解单调区间。第二问中,运用极值的问题,和直线方程的知识求解交点,得到参数的值。
(1)

已知抛物线C: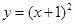 与圆
与圆 有一个公共点A,且在A处两曲线的切线与同一直线l
有一个公共点A,且在A处两曲线的切线与同一直线l
(I) 求r;
(II) 设m、n是异于l且与C及M都相切的两条直线,m、n的交点为D,求D到l的距离。
【解析】本试题考查了抛物线与圆的方程,以及两个曲线的公共点处的切线的运用,并在此基础上求解点到直线的距离。
【点评】该试题出题的角度不同于平常,因为涉及的是两个二次曲线的交点问题,并且要研究两曲线在公共点出的切线,把解析几何和导数的工具性结合起来,是该试题的创新处。另外对于在第二问中更是难度加大了,出现了另外的两条公共的切线,这样的问题对于我们以后的学习也是一个需要练习的方向。

(本小题满分12分)
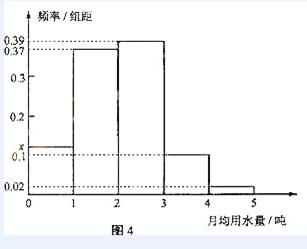
图4是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图
(Ⅰ)求直方图中x的值
(II)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用水量在3至4吨的居民数X的分布列和数学期望。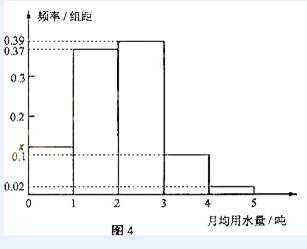
一、1――12 DBDCD CABAC DD
二、13.810 14. 6 15. 420 16. 
三、解答题
17.解(I)由 ,得
,得
由 ,得
,得
又
所以
(II)由正弦定理得
所以 的面积
的面积
18.解:

(I)
有 6中情况
6中情况
所以函数 有零点的概率为
有零点的概率为
(II)对称轴 ,则
,则

 函数
函数 在区间
在区间 上是增函数的概率为
上是增函数的概率为
 19.解:(I)证明:由已知得:
19.解:(I)证明:由已知得:




 (II)证明:取AB中点H,连结GH,FH,
(II)证明:取AB中点H,连结GH,FH,


 (由线线平行证明亦可)
(由线线平行证明亦可)
 (III)
(III)

 20.解(I)
20.解(I)


 (II)
(II)


 若
若 时,
时, 是减函数,则
是减函数,则 恒成立,得
恒成立,得


 (若用
(若用 ,则必须求导得最值)
,则必须求导得最值)
 21.解:(I)由
21.解:(I)由 ,得
,得
 解得
解得 或
或 (舍去)
(舍去)


 (II)
(II)


 22.(I)由题设
22.(I)由题设 ,及
,及 ,
, 不妨设点
不妨设点 ,其中
,其中 ,于点A 在椭圆上,有
,于点A 在椭圆上,有 ,即
,即 ,解得
,解得 ,得
,得
 直线AF1的方程为
直线AF1的方程为 ,整理得
,整理得
 由题设,原点O到直线AF1的距离为
由题设,原点O到直线AF1的距离为 ,即
,即
 将
将 代入上式并化简得
代入上式并化简得 ,得
,得
 (II)设点D的坐标为
(II)设点D的坐标为
 当
当 时,由
时,由 知,直线
知,直线 的斜率为
的斜率为 ,所以直线
,所以直线 的方程为
的方程为

 或
或 ,其中,
,其中,
 点
点 ,的坐标满足方程组
,的坐标满足方程组
 将①式代入②式,得
将①式代入②式,得
 整理得
整理得
 于是
于是
 由①式得
由①式得


 由
由 知
知 ,将③式和④式代入得
,将③式和④式代入得


 将
将 代入上式,整理得
代入上式,整理得
 当
当 时,直线
时,直线 的方程为
的方程为 ,
, 的坐标满足方程组
的坐标满足方程组

 ,所以
,所以 ,由
,由 知,
知,
 即
即 ,解得
,解得 ,这时,点D的坐标仍满足
,这时,点D的坐标仍满足
 综上,点D的轨迹方程为
综上,点D的轨迹方程为


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com