
题目列表(包括答案和解析)
对于正整数![]() ,用
,用![]() 表示
表示![]() 的最大奇因数,如:
的最大奇因数,如:![]() ,……. 记
,……. 记![]() ,其中
,其中![]() 是正整数.
是正整数.
(I)写出![]() ,
,![]() ,
,![]() ,并归纳猜想
,并归纳猜想![]() 与
与![]()
![]() N)的关系式;
N)的关系式;
(II)证明(I)的结论;
(Ⅲ)求![]() 的表达式.
的表达式.
设F(1,0),点M在x轴上,点P在y轴上,且
(1)当点P在y轴上运动时,求点N的轨迹C的方程;
(2)设 是曲线C上的点,且
是曲线C上的点,且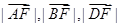 成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
【解析】本试题主要是对于圆锥曲线的综合考查。首先求解轨迹方程,利用向量作为工具表示向量的坐标,进而达到关系式的求解。第二问中利用数列的知识和直线方程求解点的坐标。
某港口的水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是水深数据:
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
根据上述数据描出的曲线如下图所示,经拟合,该曲线可近似地看成正弦函数y=Asinωt+b的图象.

(1)试根据以上数据,求出y=Asinωt+b的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间(忽略进出港所用的时间)?
已知函数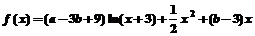 .(参考:
.(参考: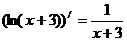 )
)
(1)当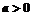 且
且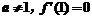 ,时,试用含
,时,试用含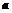 的式子表示
的式子表示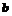 ,并讨论
,并讨论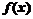 的单调区间;
的单调区间;
(2)若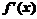 有零点,
有零点,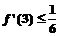 ,且对函数定义域内一切满足|x|≥2的实数x有
,且对函数定义域内一切满足|x|≥2的实数x有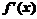 ≥0.
≥0.
①求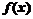 的表达式;
的表达式;
②当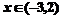 时,求函数
时,求函数 的图象与函数
的图象与函数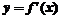 的图象的交点坐标.
的图象的交点坐标.
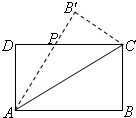 如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x.
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com