已知函数，[-2，2]表示的曲线过原点，且在x＝±1处的切线斜率均为-1，有以下命题：① f(x)的解析式为：，[-2，2]；

② f(x)的极值点有且仅有一个；

③ f(x)的最大值与最小值之和等于零；

其中正确的命题个数为（ 　）

A、0个　　　　 B、1个　　　　 C、2个　　　　 D、3个

对于定义在R上的函数f(x),有下述命题:

       ①若f(x)为奇函数,则的图象关于点A(1,0)对称;

       ②若对x∈R,有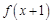＝,则f(x)的图象关于直线x＝1对称;

       ③若函数的图象关于直线x＝1对称,则f(x)为偶函数;

       ④函数与函数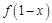的图象关于直线x＝1对称.

    其中正确命题的序号是______________.[

(文)已知函数f(x)的导数为f′(x)，若f′(x)<0(a <x <b)且f(b)>0，则在(a ，b)内必有(　)

A.f(x)＝0        B.f(x)>0         C.f(x)<0  D.不能确定

(1)对满足-1≤a≤1的一切a的值，都有g(x)＜0，求实数x的取值范围；

(2)设a=-m²，当实数m在什么范围内变化时，函数y=f(x)的图象与直线y=3只有一个公共点.