
题目列表(包括答案和解析)
 ,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答:
,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答: )2+
)2+ ,
, 时,u有最大值,umax=
时,u有最大值,umax= ,显然u没有最小值,
,显然u没有最小值, 时,g(x)有最小值4,没有最大值.
时,g(x)有最小值4,没有最大值. ,请提出此问题的一个结论,例如:求通项an.并给出正确解答.
,请提出此问题的一个结论,例如:求通项an.并给出正确解答.| 1 |
| f(x) |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| f(n) |
| 2n-1 |
已知数列{an}中,a1 = t
(t≠0,且t≠1),a2 = t2.且当x = t时,函数f (x) =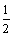 (an
– an – 1)x2 – (an
+ 1 – an) x (n≥2)取得极值.
(an
– an – 1)x2 – (an
+ 1 – an) x (n≥2)取得极值.
(1)求证:数列{an + 1 – an}是等比数列;
(2)若bn = an ln |an| (n∈N+),求数列{bn}的前n项的和Sn;
(3)当t = –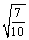 时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
(本题13分)已知数列{an}中,a1 = t (t≠0,且t≠1),a2 = t2.且当x = t时,函数f (x) =![]() (an an 1)x2 (an + 1 an) x (n≥2)取得极值.
(an an 1)x2 (an + 1 an) x (n≥2)取得极值.
(1)求证:数列{an + 1 an}是等比数列;
(2)若bn = an ln |an| (n∈N+),求数列{bn}的前n项的和Sn;
(3)当t = ![]() 时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
 (an-an-1)x2-(an+1-an)x(n≥2)取得极值?
(an-an-1)x2-(an+1-an)x(n≥2)取得极值?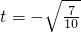 时,数列{bn}中是否存在最大项?如果存在,说明是第几项;如果不存在,请说明理由?
时,数列{bn}中是否存在最大项?如果存在,说明是第几项;如果不存在,请说明理由?一、选择题(本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中有且仅有一个符合题目要求的)
题号
1
2
3
4
5
6
7
8
答案
B
D
C
C
B
A
C
B
二、填空题(本大题共有6个小题,每小题5分,共30分;请把答案填在相应的位置)
题号
9
10
11
12
13
14
答案
-1+
8,70
24


①③④
三、解答题(本大题共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤)
15.(本题满分13分)
解:(1)


(2)由题意,得

16.(本题满分13分)
解:(1)这3封信分别被投进3个信箱的概率为

(2)恰有2个信箱没有信的概率为

(3)设信箱 中的信箱数为
中的信箱数为


0
1
2
3





17.(本题满分13分)
解:解答一:(1)在菱形 中,连接
中,连接 则
则 是等边三角形。
是等边三角形。

(2)



(3)取 中点
中点 ,连结
,连结

解法二:(1)同解法一;
(2)过点 作
作 平行线交
平行线交 于
于 ,以点
,以点 为坐标原点,建立如图的坐标系
为坐标原点,建立如图的坐标系

 二面角
二面角 的大小为
的大小为
(3)由已知,可得点

即异面直线 所成角的余弦值为
所成角的余弦值为
18.(本题满分13分)
解:(1)将函数 的图象向右平移一个单位,得到函数
的图象向右平移一个单位,得到函数 的图象,
的图象,
 函数
函数 的图象关于点(0,0)对称,即函数
的图象关于点(0,0)对称,即函数 是奇函数,
是奇函数,


由题意得:
所以
(2)由(1)可得
故设所求两点为

 满足条件的两点的坐标为:
满足条件的两点的坐标为:
(3)


19.(本题满分14分)
解:(1)椭圆 的右焦点
的右焦点 的坐标为(1,0),
的坐标为(1,0),

(2)

(3)由(2)知

20.(本题满分14分)
解:(1)

(2)由(1)知

(3)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com