
题目列表(包括答案和解析)
| 7 |
| 2 |
| 7 |
| 2 |
| p | 4 |
| 16 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| p |
| 2 |
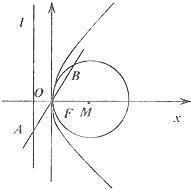 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,⊙M的圆心在x轴的正半轴上,且与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,⊙M的圆心在x轴的正半轴上,且与y轴相切,过原点O作倾斜角为| π | 3 |
| p |
| 4 |
第1卷
一、选择题(每小题5分,满分50分。)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
A
D
C
D
B
C
A
D
二、填空题(每小题2分,满分10分。)
11. 13 12. 
三、解答题(4题,满分40分)
13. m ≥ 3 或 1 < m ≤ 2
14. (1) (2)
(2) 
15. (1)
(2)最大值  ;最小值
;最小值 
16. (1)A(-2 ,1)、 B(4, 4) (2)P( 1, ) ,
) ,
第2卷
17、 6 18、 4 19、 D 20、 C
21.(1)a = 16 ; (2)增区间:(-1,1),(3,+∞);减区间:(1,3)
22.(1) (2)
(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com