题目列表(包括答案和解析)
| L/m | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
在验证“机械能守恒定律”的实验中，打点计时器所用的电源频率为50赫兹，当地的重力加速度值为9.8 m/s2，所用重物的质量为1 kg．甲、乙两位同学分别用同一装置打出两条纸带，并依次量出第1、2两点间的距离分别为0.18 cm和0.25 cm，可以看出同学操作上有错误，错误的原因是________．若按实验要求，应选________同学打出的纸带进行测量，若量得连续三点A、B、C到第一点的距离分别为15.55 cm；19.20 cm；23.23 cm．由此可知，重物运动到B点时重力势能的减少量是J，重物运动到B点时动能的增加量是________J(小数点后面保留二位数字)．
图
若按实验要求正确地选出纸带进行测量，量得连续三点A、B、C到第一个点的距离如图
（1）纸带的________端与重物相连；
（2）打点计时器打下计数点B时，物体的速度vB=________;
（3）从起点O到打下计数点B的过程中重力势能减少量是ΔEp=________，此过程中物体动能的增加量ΔEk=________（取g=
（4）通过计算，数值上ΔEp________ΔEk（填“＞”“=”或“＜”），这是因为_____________；
（5）实验的结论是______________________________________________________.
若按实验要求正确地选出纸带进行测量，量得连续三点A、B、C到第一个点的距离如图所示（相邻计数点的时间间隔为0.02 s），那么，
（1）纸带的___________端与重物相连；
（2）打点计时器打下计数点B时，物体的速度vb=___________；
（3）从起点O到计数点B的过程中重力势能减少量ΔEp=___________,此过程中物体动能的增加量ΔEk=___________；（取g=
（4）通过计算，ΔEp___________ΔEk（填“＞”“=”或“＜”＝，这是因为___________；
（5）实验的结论是___________.
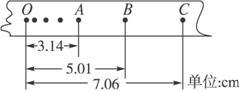
在“验证机械能守恒定律”的实验中，打点计时器所用电源频率为50 Hz，当地重力加速度的值为9.80 m/s2，测得所用重物的质量为1.00 kg.
若按实验要求正确地选出纸带进行测量，量得连续三点A、B、C到第一个点的距离如图所示（相邻计数点时间间隔为0.02 s），那么，
（1）纸带的________端与重物相连；
（2）打点计时器打下计数点B时，物体的速度vB=________；
（3）从起点O到打下计数点B的过程中重力势能减少量是ΔEp=___________，此过程中物体动能的增加量ΔEk=________（取g=9.8 m/s2）;
（4）通过计算，数值上ΔEp________ΔEk（填“＞”“=”或“＜”），这是因为________；
（5）实验的结论是________.
第Ⅰ卷 （选择题 共48分）
一、单项选择题（本题共10小题，每小题3分，共30分）。
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
A
D
C
B
B
B
A
D
二、多项选择题（本题共6小题，每小题3分，共18分。每小题给出的四个选项中，有一个或多个选项正确。全部选对的得3分，选对但不全的得2分，有选错的得0分）。
题号
11
12
13
14
15
16
答案
AD
BD
AD
ABC
AD
BCD
第Ⅱ卷 （实验题、计算题，共7题，共72分）
三、实验题（18分）
17.（1）0.730；8.0（8也给分）；
；（前两空分别为2分，第三空4分）
（2）l1、l3；
（每空2分）
（3）①乙；②9.4；③纸带和打点计时器间的摩擦阻力、空气阻力（每空2分）
四、计算题：本题共6小题，共54分。解答应有必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的，答案中必须写出数值和单位。
18.（8分）分析和解：
（1）因为金属块匀速运动，所以
Fcos37°－
（mg－Fsin37°）＝0 ……………………………………………（2分）
＝
＝
＝0.4 ……………………………（2分）
（2）撤去拉力后a＝
＝g …………………………………………………（1分）
a＝
金属块在桌面上滑行的最大距离s＝
…………………………………（1分）
＝
………………………………（1分）
s＝
19.（8分）分析和解：
（1）导体棒、金属导轨和直流电源构成闭合电路，根据闭合电路欧姆定律有：
I＝
＝
（2）导体棒受到的安培力：
F安＝BIL＝0.30 N …………………………………………………………（2分）
（3）导体棒所受重力沿斜面向下的分力F1＝mgsin37°＝0.24 N
由于F1小于安培力，故导体棒受沿斜面向下的摩擦力f ………………（1分）
根据共点力平衡条件mgsin37°＋f＝F安 …………………………………（1分）
解得：f＝0.06 N …………………………………………………………（1分）
20.（8分）分析和解：
（1）带电粒子经过电场加速，进入偏转磁场时速度为v，由动能定理
qU＝
mv2 ………………………………………………………………①（1分）
进入磁场后带电粒子做匀速圆周运动，轨道半径为r
qvB＝m
………………………………………………………………②（2分）
打到H点有r＝
………………………………………………………③（1分）
由①②③得
＝
…………………………………………………（1分）
（2）要保证所有带电粒子都不能打到MN边界上，带
电粒子在磁场中运动偏角小于90°，临界状态为
90°。如图所示，磁场区半径R＝r＝ （2分）
所以磁场区域半径满足R≤
（1分）
21.（10分）分析和解：
（1）木块A在桌面上受到滑动摩擦力作用做匀减速运动，根据牛顿第二定律，木
块A的加速度a＝
＝
设两木块碰撞前A的速度大小为v，根据运动学公式，得
v＝v0－at＝
（2）两木块离开桌面后均做平抛运动，设木块B离开桌面时的速度大小为v2，在空
中飞行的时间为t′。根据平抛运动规律有：h＝gt′2，s＝v2t′ …………（2分）
解得：v2＝
＝
（3）设两木块碰撞后木块A的速度大小为v1，根据动量守恒定律有：
Mv＝Mv1＋mv2 ………………………………………………………（1分）
解得：v1＝
＝
设木块A落到地面过程的水平位移为s′，根据平抛运动规律，得
s′＝v1t′＝v1
＝
则木块A落到地面上的位置与D点之间的距离
s＝s－s′＝
22.（10分）分析和解：
（1）设电子经电压U1加速后的速度为v0，由动能定理eU1＝
－0 ……（2分）
解得v0＝
…………………………………………………………（1分）
（2）电子以速度v0进入偏转电场后，垂直于电场方向做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动。设偏转电场的电场强度为E，电子在偏转电场中运动的时间为t，加速度为a，电子离开偏转电场时的侧移量为y。由
牛顿第二定律和运动学公式t＝
………………………………………（1分）
F＝ma F＝eE E＝
a＝
……………………………………（2分）
y＝ at2 ……………………………………………………………………（1分）
解得y＝
……………………………………………………………（1分）
（3）减小加速电压U1；增大偏转电压U2；……
（本题的答案不唯一，只要措施合理，答出一项可得1分，答出两项及以上可得2分。）
23.（10分）分析和解：
（1）设轨道半径为R，由机械能守恒定律：
mv2B＝mg（2R＋x）＋ mv
在B点：
－mg＝m
……………………………………………………②（1分）
在A点：
＋mg＝m
……………………………………………………③（1分）
由①②③式得：两点的压力差，FN＝－＝6 mg＋
………④（1分）
由图象得：截距6 mg＝6，得m＝
（2）由④式可知：因为图线的斜率k＝
＝1
所以R＝
（3）在A点不脱离的条件为：vA≥
………………………………………⑦（1分）
由①⑥⑦三式和题中所给已知条件解得：x＝
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com