练习册

  • 练习册
  • 试题
    21．设双曲线的左.右焦点分别为F1.F2.P是双曲线右支上一点.△PF1F2的内切圆与x轴切于点Q(1.0).且|F1Q| = 4．(1)求双曲线的方程, 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分13分)

    设双曲线，点A、B分别为双曲线C实轴的左端点和虚轴的上端点，点、分别为双曲线C的左、右焦点，点M、N是双曲线C的右支上不同两点，点Q为线段MN的中点．已知在双曲线C上存在一点P，使得．

    （Ⅰ）求双曲线C的离心率；

    （Ⅱ）设为正常数，若点Q在直线上，求直线MN在y轴上的截距的取值范围.　

    查看答案和解析>>

    （本小题满分13分）

      如图，已知椭圆的离心率为，以该椭圆上的点和椭圆的

      左、右焦点为顶点的三角形的周长为.一等轴双曲线的顶点是该椭

      圆的焦点，设为该双曲线上异于顶点的任一点，直线和与椭圆的交点

      分别 为和

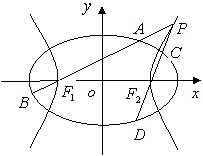       （Ⅰ）求椭圆和双曲线的标准方程； 

       （Ⅱ）设直线、的斜率分别为、，证明；

       （Ⅲ）是否存在常数，使得恒成立？

          若存在，求的值；若不存在，请说明理由.

                                                                 

    查看答案和解析>>

    （本小题满分13分）已知焦点在x轴上的双曲线C的两条渐近线相交于坐标原点，且两条渐近线与以点为圆心，1为半径的圆相切，又知双曲线C的一个焦点与点A关于直线y=x对称.

    （1）求双曲线C的标准方程；

    （2）若Q是双曲线C上的任一点，F1、F2分别是双曲线C的左、右焦点，从点F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程.

    （3）设直线y=mx+1与双曲线C的左支交于A、B两点，另一直线L经过点M（－2，0）和线段AB的中点，求直线L在y轴上的截距b的取值范围

    查看答案和解析>>

    一、选择题：B B AD C/  BDBCB

    二、填空题：

    11、10     12、3     13、21    14、4     15、

    三、解答题：

    16、【解析】(1)……………………3分

    的最小正周期;……………………6分

    (2) 将函数f(x)沿向量得到函数g(x)= ……9分

    当即 时，函数g(x)单调递减，

    故所求区间为.………………………………………12分

    17、解：∵∴

      ①…………5分

    又∵

    ∴②……10分

    由①②知，即a的取值集合M=[2，3].……………………12分

    18、【解析】（1）证明：由已知AE⊥面CDO，，所以CD⊥AE

    又CD⊥AD，AD∩AE =A

    故CD⊥平面ADE，

    故平面ABCD⊥平面ADE；…………………………………………4分

    （2）由（1）知CD⊥AD，CD⊥ED，

    故∠ADE为二面角A-CD-E的平面角．…………………………………………6分

    在Rt△ADE中，sin∠ADE=,∠ADE=

    故平面ABCD与平面CDE所成角的平面角的大小为……………………………………8分

    （3）凸多面体ABCDE为四棱锥E?ABCD，VE?ABCD = ．………………………………12分

     

    19、【解析】（1）由b2＜a3，得ab＜a + 2b．………………………………1分

    ∵1＜a＜b，∴ab＜3b，则1＜a＜3．………………………………3分

    又a为正整数，∴a = 2．………………………………4分

    ∵am + 1 = bn，∴2 + (m ? 1)b + 1 = b?2n ? 1．

    ∴b =．………………………………6分

    ∵b∈N*，2 n ? 1 ? m + 1 = 1．

    故b = 3．………………………………8分

    （2）∵an = 2 + (n ? 1)?3 = 3n ? 1，b2n + 1 = 3?22n，………………………………10分

    ∴cn ==．

    ∴当n = 2或n = 3时，cn取得最小值，最小值为?12．………………………………13分

    20、【解析】（1）依题意，f ′(1) = -1 + 2b + c = 0，f ′(m) = -m2 + 2bm + c = 1．………………………1分

    ∵-1＜b＜c，∴-4＜-1+ 2b + c＜4c，∴c＞0．

    将c = 1 ? 2b代入-1＜b＜c，得?1＜b＜．………………………………3分

    将c = 1? 2b代入-m2 + 2bm + c = 1，得 -m2 + 2bm ? 2b = 0．

    由= 4b2 - 8b≥0，得b≤0或b≥2．………………………………5分

    综上所述，-1＜≤0．………………………………6分

    （2）由f′(x)＜1，得 -x2 + 2bx ? 2b＜0．

    ∴x2 ，………………………………8分

    易知为关于的一次函数．………………………………9分

    依题意，不等式g()＞0对-1＜≤0恒成立，

    ∴得x≤或x≥．………………………………12分

    ∴k≥，即k的最小值为．………………………………13分

    21、【解析】（1）设△PF1F2的内切圆与PF1、PF2的切点分别为D、E，则|PD| = |PE|，|F1D| =|F1Q|，

    |F2E| = |F2Q|．

    ∵|PF1| ? |PF2| = 2a，∴|F1Q| ? |F2Q| = 2a，

    ∴Q(1，0)为双曲线的右顶点，即a = 1．………………………………3分

    又|F1Q| = a + c = 4，∴c = 3，则b2 = c2 ? a2 = 8．

    故双曲线方程为．………………………………5分

    （2）设R(t≠0)、N(x0，y0)，由R、B、N三点共线，得，即=，于是解得，则R．………………………………6分

    ∵，，

    ∴．………………………………8分

    又点N在双曲线上，∴．

    ∴．………………………………9分

    ∵x0≥1，∴AN?AR＜0，∴∠RAN为钝角．

    又∠RAN与∠MAN互补，∴∠MAN为锐角．………………………………11分

    故点A在以MN为直径的圆的外部．………………………………13分

     

     

     

     


    同步练习册答案