练习册

  • 练习册
  • 试题
    求导易得当时有面积的最大值． --------13分 【查看更多】

     

    题目列表(包括答案和解析)

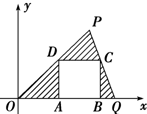    精英家教网t∈R，且t∈（0，10），由t确定两个任意点P（t，t），Q（10-t，0）．
    （1）直线PQ是否能通过下面的点M（6，1），点N（4，5）；
    （2）在△OPQ内作内接正方形ABCD，顶点A、B在边OQ上，顶点C在边PQ上，顶点D在边OP上．
    ①求证：顶点C一定在直线y=
    12
    x上．
    ②求下图中阴影部分面积的最大值，并求这时顶点A、B、C、D的坐标．

    查看答案和解析>>

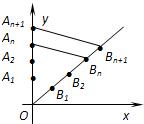    精英家教网如图，在y轴的正半轴上依次有点A1，A2，…，An，…其中点A1（0，1），A2（0，10），且|An-1An|=3|AnAn+1|（n=2，3，4，…），在射线y=x（x≥0）上依次有点B1，B2，…，Bn，…点B1的坐标为（3，3），且|OBn|=|OBn-1|+2
    		2
    （n=2，3，4，…）
    （1）用含n的式子表示|AnAn+1|；
    （2）用含n的式子表示An，Bn的坐标；
    （3）求四边形AnAn+1Bn+1Bn面积的最大值．

    查看答案和解析>>

    （2004•黄冈模拟）已知
    i
    ，
    j
    分别是x轴，y轴方向上的单位向量，
    OA1
    =
    j
    ，
    OA2
    =10
    j
    ，且
    An-1An
    =3
    AnAn+1
    (n=2，3，4，…)    ，在射线y=x（x≥0）上从下到上依次有点Bi=（i=1，2，3，…），
    OB1
    =3
    i
    +3
    j
    且|
    Bn-1Bn
    |=2
    		2
    （n=2，3，4…）．
    （Ⅰ）求
    A4A5
    ；
    （Ⅱ）求
    OAn
    ，
    OBn
    ；
    （III）求四边形AnAn+1Bn+1Bn面积的最大值．

    查看答案和解析>>

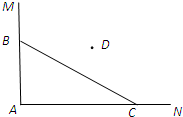    在一个矩形体育馆的一角MAN内（如图所示），用长为a的围栏设置一个运动器材储存区域，已知B是墙角线AM上的一点，C是墙角线AN上的一点．
    （1）若BC=a=10，求储存区域三角形ABC面积的最大值；
    （2）若AB=AC=10，在折线MBCN内选一点D，使DB+DC=a=20，求储存区域四边形DBAC面积的最大值．

    查看答案和解析>>

    已知椭圆的四个顶点恰好是一边长为2，一内角为的菱形的四个顶点.

    （I）求椭圆的方程；

    （II）直线与椭圆交于，两点，且线段的垂直平分线经过点，求（为原点）面积的最大值.

     

    查看答案和解析>>


    同步练习册答案