
题目列表(包括答案和解析)
将![]() 边长为
边长为![]() 的菱形
的菱形![]() 沿对角线
沿对角线![]() 折成大小等于
折成大小等于![]() 的二面角
的二面角![]() .
.
若![]() ,
,![]() 分别为
分别为![]() 的中点,则下列说法中正确的有
的中点,则下列说法中正确的有
①![]() ②
②![]() 与平面
与平面![]() 所成角为
所成角为![]() ③线段
③线段![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]()
④当![]() 时,
时,![]() 与
与![]() 所成角等于
所成角等于![]()
将![]() 边长为
边长为![]() 的菱形
的菱形![]() 沿对角线
沿对角线![]() 折成大小等于
折成大小等于![]() 的二面角
的二面角![]() .
.
若![]() ,
,![]() 分别为
分别为![]() 的中点,则下列说法中正确的有
的中点,则下列说法中正确的有
①![]() ②
②![]() 与平面
与平面![]() 所成角为
所成角为![]() ③线段
③线段![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]()
④当![]() 时,
时,![]() 与
与![]() 所成角等于
所成角等于![]()
 如图所示,二面角α-CD-β的大小为θ,点A在平面α内,△ACD的面积为s,且CD=m,过A点的直线交平面β于B,AB⊥CD,且AB与平面β所成的角为30°,则当θ=
如图所示,二面角α-CD-β的大小为θ,点A在平面α内,△ACD的面积为s,且CD=m,过A点的直线交平面β于B,AB⊥CD,且AB与平面β所成的角为30°,则当θ=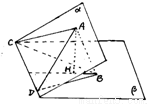
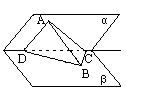
如图所示,二面角α-DC-β的大小为θ,A为α内一定点,且△ADC的面积为S,DC=a,过A作直线AB,使AB⊥CD且与平面β成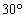 角,当θ变化时,求△DBC面积的最大值.
角,当θ变化时,求△DBC面积的最大值.
一、选择题:
1.C 2.D 3.D 4.C 5. B 6.C 7. C 8.C 9. A
|