
题目列表(包括答案和解析)
| 2 |
| x |
| A、(1,2) |
| B、(2,3) |
| C、(e,3) |
| D、(e,+∞) |
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=1-x2,函数g(x)=lg|x|,则函数y=f(x)与y=g(x)的图象在区间[-5,5]内的交点个数为 .
| 2 |
| x |
| A.(1,2) | B.(2,3) | C.(e,3) | D.(e,+∞) |
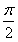 ,f(x)图象的一条对称轴是直线
,f(x)图象的一条对称轴是直线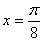 。
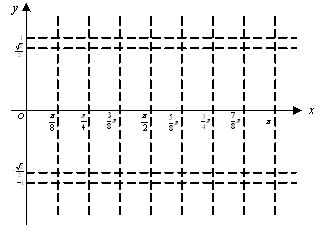
。
一、选择题:
1.C 2.D 3.D 4.C 5. B 6.C 7. C 8.C 9. A
|