
题目列表(包括答案和解析)
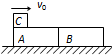 如图所示,质量均为2m的完全相同的长木板A、B并排放置在光滑水平面上静止.一个质量为m的铁块C以水平速度v0=1.8m/s从左端滑到A木板的上表面,并最终停留在长木板B上.已知B、C最终的共同速度为v=0.4m/s.求:
如图所示,质量均为2m的完全相同的长木板A、B并排放置在光滑水平面上静止.一个质量为m的铁块C以水平速度v0=1.8m/s从左端滑到A木板的上表面,并最终停留在长木板B上.已知B、C最终的共同速度为v=0.4m/s.求: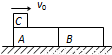
(09年东台市期末)(8分)如图所示,质量均为2m的完全相同的长木板A、B并排放置在光滑水平面上静止.一个质量为m的铁块C以水平速度v0=1.8/s从左端滑到A木板的上表面,并最终停留在长木板B上.已知B、C最终的共同速度为v=0.4m/s.求:
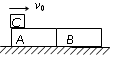
![]() ⑴A木板的最终速度v1;
⑴A木板的最终速度v1;
![]() ⑵铁块C刚离开长木板A时刻的瞬时速度v2。
⑵铁块C刚离开长木板A时刻的瞬时速度v2。
 如图所示,在一水平的长直轨道上放着两块完全相同的质量均为研的长方形木块A和B,在木块A之前放有一质量M=2m的大木块,大木块、木块A和木块B与轨道间的动摩擦因数均相同.已知大木块与木块A之间的距离与A、B两木块间的距离相同,均为L.今在所有木块都静止的情况下,将一沿轨道方向的恒力F一直作用在大木块上,使其先与木块A发生碰撞,碰后与木块A结为一体再与木块B发生碰撞.碰后又结为一体并恰能一起做匀速运动,设每次碰撞的时间极短,已知重力加速度为g,求:
如图所示,在一水平的长直轨道上放着两块完全相同的质量均为研的长方形木块A和B,在木块A之前放有一质量M=2m的大木块,大木块、木块A和木块B与轨道间的动摩擦因数均相同.已知大木块与木块A之间的距离与A、B两木块间的距离相同,均为L.今在所有木块都静止的情况下,将一沿轨道方向的恒力F一直作用在大木块上,使其先与木块A发生碰撞,碰后与木块A结为一体再与木块B发生碰撞.碰后又结为一体并恰能一起做匀速运动,设每次碰撞的时间极短,已知重力加速度为g,求:| 2 | 5 |
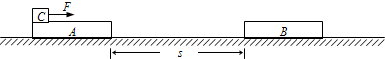
一、选择题(每小题中至少有一个答案是正确的,全对得4分,不全得2分,错与不答得0分.)
1.C 2.B D 3.B 4.D 5.A C 6.B 7.B 8.C D 9.B 10.A B D 11.A 12.A D 13.C 14.B
二、填空题(每空2分,共20分)答错、不答和答案不能辩认的为0分
15.(4分)①a=____1.93____m/s2。②v=__1.18__ m/s。(答案均要求保留3位有效数字)
16.(4分)(1)逆时针 。(2) 大
17.(6分)(1)B= IR/2πLhf 。10-5 T。 (2)0 。
18.(6分)
a b Rx= .files/image057.gif) .
.
三、计算题(8+8+8=24分)每题要写出公式,代入相应的数据,最后得出答案.(21题是选做题,只能选取一题计入总分,多答不得分)
19.
解:对A、B、C整体,从C以v0滑上木块到最终B、C达到共同速度V,其动量守恒既:
m v0=2mV1+3mv (2分)
.files/image058.gif) 1.8=2V1+3×0.4 (1分)
1.8=2V1+3×0.4 (1分)
V1=
对A、B、C整体,从C以v0滑上木块到C以V2刚离开长木板,
此时A、B具有共同的速度V1。其动量守恒既:
m v0=mV2+4mv1 (2分)
1.8=V2+4×0.3 (1分)
V2=
20.
.files/image059.gif) 解:(1)当线框上边ab进入磁场,线圈中产生感应电流I,由楞次定律
解:(1)当线框上边ab进入磁场,线圈中产生感应电流I,由楞次定律
可知产生阻碍运动的安培力为F=Bil (1分)
由于线框匀速运动,线框受力平衡,F+mg=Mg (1分)
联立求解,得I=
由欧姆定律可得,E=IR=0.16V (1分)
由公式E=Blv,可求出v=
F=BIl=0.4N (1分)
(2)重物M下降做的功为W=Mgl=0.14J (1分)
|