
题目列表(包括答案和解析)
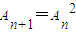 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.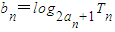 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.在各项均为正数的数列![]() 中,前
中,前![]() 项和
项和![]() 满足
满足![]() 。
。
(1)证明![]() 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前![]() 项和的公式;
项和的公式;
(2)在平面直角坐标系![]() 面上,设点
面上,设点![]() 满足
满足![]() ,且点
,且点![]() 在直线
在直线![]() 上,
上,![]() 中最高点为
中最高点为![]() ,若称直线
,若称直线![]() 与
与![]() 轴、直线
轴、直线![]() 所围成的图形的面积为直线
所围成的图形的面积为直线![]() 在区间
在区间![]() 上的面积,试求直线
上的面积,试求直线![]() 在区间
在区间![]() 上的面积;
上的面积;
(3)若存在圆心在直线![]() 上的圆纸片能覆盖住点列
上的圆纸片能覆盖住点列![]() 中任何一个点,求该圆纸片最小面积.
中任何一个点,求该圆纸片最小面积.
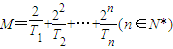 ,求证:
,求证: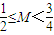 .
.选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
A
A
B
C
D
C
A
填空题
11. 12.
12. 13.-18 14.(2,3) 15.①②⑤
13.-18 14.(2,3) 15.①②⑤
16. 解(1)由题意得 , ………2分 ; 从而
, ………2分 ; 从而 , ………4分
, ………4分
又 ,所以
,所以 ………………………………………6分
………………………………………6分
(2)由(1)得 ………………………8分
………………………8分
因为 ,所以
,所以 ,所以当
,所以当 时,
时, 取得最小值为1…10分
取得最小值为1…10分
且 的单调递减区间为
的单调递减区间为 ………………………………12分
………………………………12分
17. 令 设
设 的值域为M.
的值域为M.
(Ⅰ)当 的定义域为R,有
的定义域为R,有

 .
.
故
 …………………………6分
…………………………6分
(Ⅱ)当 的值域为R,有
的值域为R,有


故 或
或
∴  ………………………………………………12分
………………………………………………12分
 18. 建立如图所示的直角坐标系,则E(30,0),F(0,20)。
18. 建立如图所示的直角坐标系,则E(30,0),F(0,20)。
∴线段 的方程是
的方程是 ………3分
………3分
在线段 上取点
上取点 ,作PQ⊥BC于点Q,PR⊥CD于点R,
,作PQ⊥BC于点Q,PR⊥CD于点R,
设矩形PQCR的面积为s,则s=|PQ|?|PR|=(100- )(80-
)(80- ).…………6分
).…………6分
又∵  ,∴
,∴ ,
,
∴ 。……10分
。……10分
∴当 =
= .
.
故当矩形广场的两边在BC、CD上,一个顶点在线段EF上,
且这个顶点分EF成5:1时,广场的面积最大。 …………12分
19.解: (1) 由题知:  , 解得
, 解得 , 故
, 故 . ………2分
. ………2分
(2)  ,
,
 ,
,
 ,
,
又 满足上式. 所以
满足上式. 所以 ……………7分
……………7分
(3) 若 是
是 与
与 的等差中项, 则
的等差中项, 则 ,
,
从而 , 得
, 得 .
.
因为 是
是 的减函数, 所以
的减函数, 所以
当 , 即
, 即 时,
时,  随
随 的增大而减小, 此时最小值为
的增大而减小, 此时最小值为 ;
;
当 , 即
, 即 时,
时,  随
随 的增大而增大, 此时最小值为
的增大而增大, 此时最小值为 .
.
又 , 所以
, 所以 ,
,
即数列 中
中 最小, 且
最小, 且 . …………12分
. …………12分
20.解:(1)三个函数的最小值依次为 ,
, ,
,
由 ,得
,得
∴
 ,
,
故方程 的两根是
的两根是 ,
, .
.
故 ,
, .
.
 ,即
,即
∴
 .………………6分
.………………6分
(2)①依题意 是方程
是方程 的根,
的根,
故有 ,
, ,
,
且△ ,得
,得 .
.
由 ……………9分
……………9分

 ;得,
;得, ,
, .
.
由(1)知 ,故
,故 ,
,
∴  ,
,
∴  .………………………13分
.………………………13分
21.(Ⅰ)设AB:x=my+2, A(x1,y1) ,B(x2,y2)
 将x=my+2代入
将x=my+2代入 ,消x整理,得:
,消x整理,得:
(m2+2)y2+4my-4=0
而
 =
=
= =
=

取“=”时,显然m=0,此时AB:x=2……………………6分
(Ⅱ)(?)显然 是椭圆
是椭圆 的右焦点,离心率
的右焦点,离心率
且
作
 点A在椭圆上
点A在椭圆上



 ……………10分
……………10分
(?)同理  ,由
,由
有  =2
=2
解得: =
= ,故
,故
所以直线AB: y= (x-2)
(x-2)
即直线AB的方程为 ………14分
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com