练习册

  • 练习册
  • 试题
    又∵∴ AC∥平面GBE．----6分 (2)解:延长EG交DA的延长线于H点.连结BH.作AO⊥GH于O点.连结BO．∵ 平面ABCD⊥平面ADEF.平面ABCD∩平面ADEF＝AD .AB⊥AD∴ AB⊥平面ADEF.由三垂线定理.知AB⊥GH.故∠AOB就是二面角B-GE-D的平面角．----8分∵ 平面ABCD⊥平面ADEF.平面ABCD∩平面ADEF＝AD .ED⊥AD∴ ED⊥平面ABCD.故∠EBD就是直线BE与平面ABCD成的角.--10分 【查看更多】

     

    题目列表(包括答案和解析)

    如图，ABCD－A1B1C1D1为正方体，下面结论中正确的是_____________.

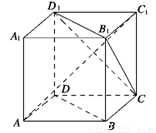    ①　AC∥平面CB1D1；

    ②　AC1⊥平面CB1D1；

    ③　AC1与底面ABCD所成角的正切值是；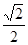

    ④　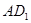与BD为异面直线。

     

     

     

    查看答案和解析>>

    （2010•昆明模拟）如图，在正方形ABCD中，E、F分别是BC、CD的中点，AC∩EF=G．现在沿AE、EF、FA把这个正方形折成一个四面体，使B、C、D三点重合，重合后的点记为P，则在四面体P-AEF中必有（　　）

    查看答案和解析>>

    在△ABC（如图1），若CE是∠ACB的平分线，则
    AC
    BC
    =
    AE
    BE
    ．其证明过程如下：
    作EG⊥AC于点G，EH⊥BC于点H，CF⊥AB于点F，
    ∵CE是∠ACB的平分线，
    ∴EG=EH．
    又∵
    AC
    BC
    =
    AC•EG
    BC•EH
    =
    S△AEC
    S△BEC
    ，
    AE
    BE
    =
    AE•CF
    BE•CF
    =
    S△AEC
    S△BEC
    ，
    ∴
    AC
    BC
    =
    AE
    BE

    （1）把上面结论推广到空间中：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，类比三角形中的结论，你得到的相应空间的结论是
    S△ACD
    S△BCD
    =
    AE
    BE
    S△ACD
    S△BCD
    =
    AE
    BE

    （2）证明你所得到的结论．

    查看答案和解析>>

    在△ABC（如图1），若CE是∠ACB的平分线，则
    AC
    BC
    =
    AE
    BE
    ．其证明过程如下：
    作EG⊥AC于点G，EH⊥BC于点H，CF⊥AB于点F，
    ∵CE是∠ACB的平分线，
    ∴EG=EH．
    又∵
    AC
    BC
    =
    AC•EG
    BC•EH
    =
    S△AEC
    S△BEC
    ，
    AE
    BE
    =
    AE•CF
    BE•CF
    =
    S△AEC
    S△BEC
    ，
    ∴
    AC
    BC
    =
    AE
    BE

    （1）把上面结论推广到空间中：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，类比三角形中的结论，你得到的相应空间的结论是______
    （2）证明你所得到的结论．

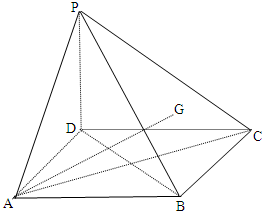    精英家教网

    查看答案和解析>>

    精英家教网如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，点G是侧面三角形PBC的重心；
    （1）求证：AC⊥平面PBD．
    （2）求AG与平面PBD所成的角的正弦值．
    （3）在侧棱PD上是否存在一点N，使得PB∥平面AGN？，若存在试确定点N的位置，若不存在，试说明理由．

    查看答案和解析>>


    同步练习册答案