
题目列表(包括答案和解析)
如图1,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() .
.
(1)动点![]() 在边
在边![]() 上运动,且与点
上运动,且与点![]() ,
,![]() 均不重合,设
均不重合,设![]()
①设
②当
(2
)如图2,以图1中的为一组邻边的矩形中,动点在矩形边上运动一周,能使是以为顶角的等腰三角形共有多少个(直接写结果,不要求说明理由)?

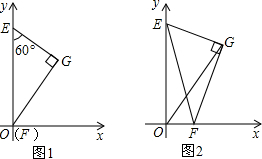
如图1,四边形ABCD中, 、
、 为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为
为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为 ,如果在点
,如果在点 的运动过程中,
的运动过程中, 的值不变,则我们称四边形ABCD为“
的值不变,则我们称四边形ABCD为“ 四边形”, 此时
四边形”, 此时 的值称为它的“
的值称为它的“ 值”.经过探究,可得矩形是“
值”.经过探究,可得矩形是“ 四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“
四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“ 值”为 .
值”为 .
(1)等腰梯形 (填“是”或 “不是”)“ 四边形”;
四边形”;
(2)如图3, 是⊙O的直径,A是⊙O上一点,
是⊙O的直径,A是⊙O上一点,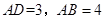 ,点
,点 为
为 上的一动点,将△
上的一动点,将△ 沿
沿 的中垂线翻折,得到△
的中垂线翻折,得到△ .当点
.当点 运动到某一位置时,以
运动到某一位置时,以 、
、 、
、 、
、 、
、 、
、 中的任意四个点为顶点的“
中的任意四个点为顶点的“ 四边形”最多,最多有 个.
四边形”最多,最多有 个.
如图1,四边形ABCD中, 、
、 为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为
为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为 ,如果在点
,如果在点 的运动过程中,
的运动过程中, 的值不变,则我们称四边形ABCD为“
的值不变,则我们称四边形ABCD为“ 四边形”,
此时
四边形”,
此时 的值称为它的“
的值称为它的“ 值”.经过探究,可得矩形是“
值”.经过探究,可得矩形是“ 四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“
四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“ 值”为 .
值”为 .

(1)等腰梯形 (填“是”或 “不是”)“ 四边形”;
四边形”;
(2)如图3, 是⊙O的直径,A是⊙O上一点,
是⊙O的直径,A是⊙O上一点, ,点
,点 为
为 上的一动点,将△
上的一动点,将△ 沿
沿 的中垂线翻折,得到△
的中垂线翻折,得到△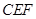 .当点
.当点 运动到某一位置时,以
运动到某一位置时,以 、
、 、
、 、
、 、
、 、
、 中的任意四个点为顶点的“
中的任意四个点为顶点的“ 四边形”最多,最多有 个.
四边形”最多,最多有 个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com