练习册

  • 练习册
  • 试题
    (2)将图2中的绕点顺时针旋转.使点落在上.连结．请找出图中的全等三角形.并说明它们全等的理由．(不再添加辅助线.不再标注其它字母)． 【查看更多】

     

    题目列表(包括答案和解析)

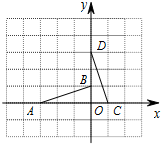    作业宝如图，已知△OAB的顶点A（-3，0）、B（0，1）O（0，0）．将△OAB绕点O按顺时针旋转90°得到△ODC，抛物线y=ax2+bx+c经过A、D、C三点．
    （1）求抛物线的解析式，并写出抛物线的顶点坐标；
    （2）在给定的平面直角坐标中，画出（1）中抛物线；
    （3）将（1）中的抛物线沿y轴平移m（m＞0）个长度单位，使平移后抛物线的顶点落在直线y=-x上，试求出平移的方法和平移后的抛物线的解析式．

    查看答案和解析>>

    在ABC中，AB=BC，将ABC绕点A沿顺时针方向旋转得A1B1C1，使点Cl落在

    直线BC上(点Cl与点C不重合)，

    (1)如图9一①，当C>60°时，写出边ABl与边CB的位置关系，并加以证明；

    (2)当C=60°时，写出边ABl与边CB的位置关系(不要求证明)；

    (3)当C<60°时，请你在图9一②中用尺规作图法作出△AB1C1(保留作图痕迹，不写作法)，再猜想你在(1)、(2)中得出的结论是否还成立?并说明理由．

    　

    查看答案和解析>>

    （2012•和平区模拟）图①至图③中，两平行线AB、CD间的距离均为6，点M为AB上一定点．扇形纸片OMP在AB、CD之间（包括AB、CD），扇形OMP的圆心角∠MOP=α，半径OM=4．如图①，扇形的半径OM在AB上．如图②③，将扇形纸片OMP绕点M在AB、CD之间顺时针旋转．
    （Ⅰ）如图②，当α=60°时，在旋转过程中，点P到直线CD的最小距离是
    2
    2
    ，旋转角∠BMO的最大值是
    90°
    90°
    ；
    （Ⅱ）如图③，在扇形纸片OMP旋转的过程中，要使点P落在直线CD上，α的最大值是
    120°
    120°
    ．

    查看答案和解析>>

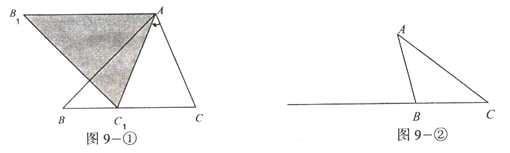
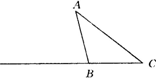
    在△ABC中，AB＝BC，将△ABC绕点A沿顺时针方向旋转得到△AB1C1，使点C1落在直线BC上(点C1与点C不重合)，

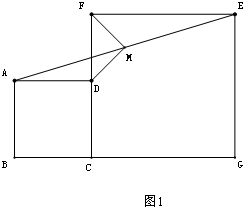
    (1)如图，当∠C＞60°，写出边AB1与边CB的位置关系，并加以证明；

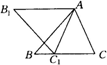
    (2)当∠C＝60°时，写出边AB1与边CB的位置关系(不要求证明)；

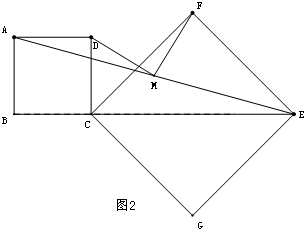
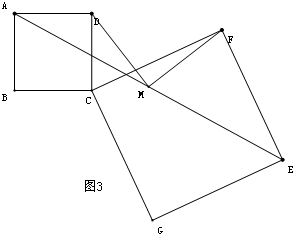
    (3)当∠C＜60°，请你在下图中用尺规作图法作出△AB1C1(保留作图痕迹，不写作法)，再猜想你在(1)、(2)中得出的结论是否成立？并说明理由．

    查看答案和解析>>

    22、如图1，点C位线段BG上一点，分别以BC、CG为边向外作正方形BCDA和正方形CGEF，使点D落在线段FC上，连接AE，点M位AE中点
    （1）求证：MD=MF，MD⊥MF
    （2）如图2，将正方形CGEF绕点C顺时针旋转45°，其他条件不变，探究：线段MD、MF的关系，并加以证明；
    （3）如图3，将正方形AGEF绕点C旋转任意角度后，其他条件不同，探究：线段MD、MF的关系，并加以证明．

    查看答案和解析>>


    同步练习册答案