
题目列表(包括答案和解析)
如图,正方形ABCD的边长为4,在AB、AD边上分别取点 P、S,连结PS,将Rt△SAP绕正方形中心O旋转180°得Rt△QCR,从而得四边形PQRS,回答以下问题(只写出结论,不必证明):
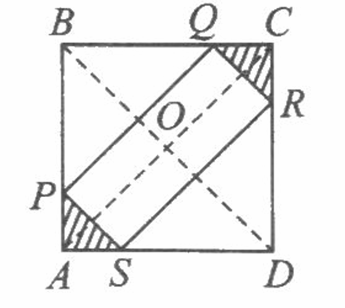
(1)四边形PQRS的形状是 __________ ;
(2)当PA与SA满足关系式 __________ 时,四边形PQRS为矩形(不是正方形),请在图中画出一个符合要求的图形;
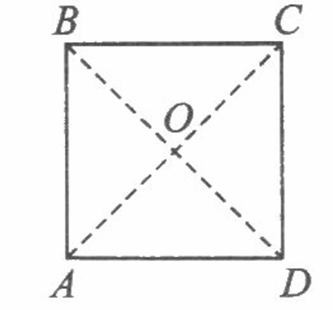
(3)当PA与SA满足关系式 __________ 时,四边形PQRS为正方形,请在图中画出一个符合要求的图形;
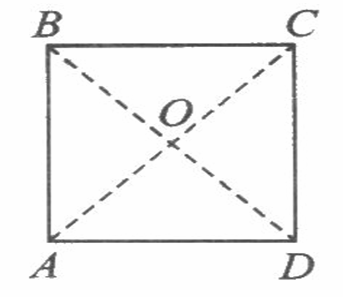
(4)上述四边形PQRS能否为不是正方形的菱形 __________ (填撃軘或摬荒軘).
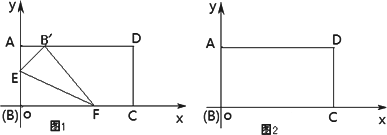
已知矩形ABCD如图放置,将矩形折叠,使B落在边AD(含端点)上,落点记为![]() ,折痕与线段AB交于E,与边BC或者边CD(含端点)交于F,则以E、B、
,折痕与线段AB交于E,与边BC或者边CD(含端点)交于F,则以E、B、![]() 为顶点的三角形ΔBB/E称为矩形ABCD的“折叠三角形”.
为顶点的三角形ΔBB/E称为矩形ABCD的“折叠三角形”.
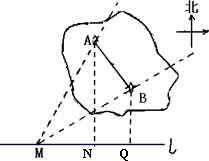
(1)由折叠三角形定义可知,矩形ABCD的任意一个折叠ΔBEB/都是一个________三角形.
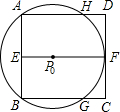
(2)在矩形ABCD中,AB=6,AD=10,当F与点C重合时,在下图中画出这个折叠ΔBE![]() ,试求点B/的坐标并求这个折叠ΔBE
,试求点B/的坐标并求这个折叠ΔBE![]() 的面积.
的面积.
 装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.| 2 |
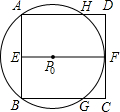 装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点. -2)平方千米,当(探测装置)P从点P0出发继续前行多少千米到达点P1处时,A、B、C、D四点恰好在⊙P1上.
-2)平方千米,当(探测装置)P从点P0出发继续前行多少千米到达点P1处时,A、B、C、D四点恰好在⊙P1上.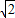 -2)平方千米,当(探测装置)P从点P出发继续前行多少千米到达点P1处时,A、B、C、D四点恰好在⊙P1上.
-2)平方千米,当(探测装置)P从点P出发继续前行多少千米到达点P1处时,A、B、C、D四点恰好在⊙P1上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com