
题目列表(包括答案和解析)
| 5 |
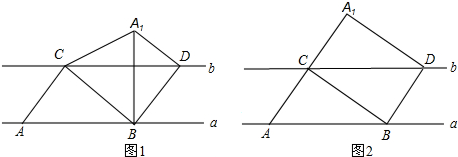
如图,在平面直角坐标系xoy中,已知直线l1:y= x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
求M,N的坐标;
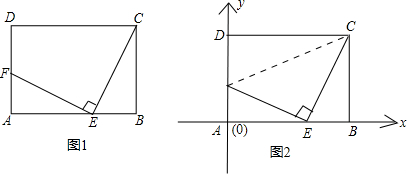
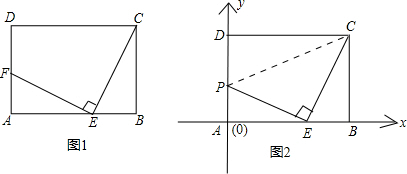
在矩形ABCD中,已知AB=1,BC=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个
单位长度的速度移动.设矩形ABCD与△OMN的重叠部分的面积为S.移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时结束)。直接写出S与自变量t之间的函数关系式(不需要给出解答过程);
在(2)的条件下,当t为何值时,S的值最大?并求出最大值.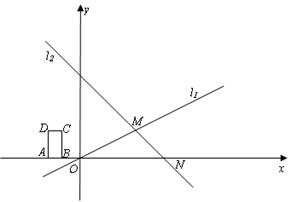
如图,在平面直角坐标系xoy中,已知直线l1:y=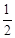 x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
求M,N的坐标;
在矩形ABCD中,已知AB=1,BC=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个
单位长度的速度移动.设矩形ABCD与△OMN的重叠部分的面积为S.移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时结束)。直接写出S与自变量t之间的函数关系式(不需要给出解答过程);
在(2)的条件下,当t为何值时,S的值最大?并求出最大值.
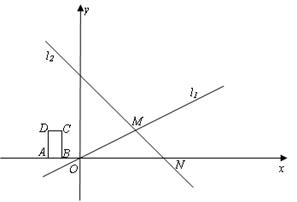
 x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.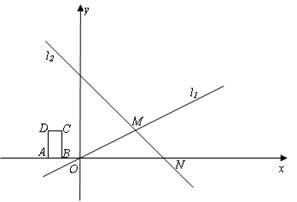
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com