
题目列表(包括答案和解析)
| 1 | 2 |
已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
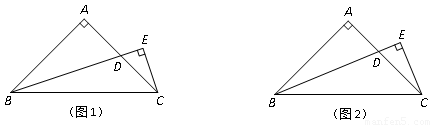
(1)若BD是AC边上的中线,如图1,求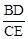 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求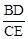 的值.
的值.
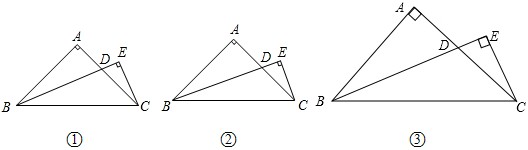
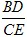 的值;
的值;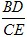 的值;
的值;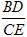 的值的取值范围(直接写出结论,不必证明),并探究
的值的取值范围(直接写出结论,不必证明),并探究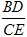 的值能小于
的值能小于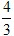 吗?若能,求出满足条件的D点的位置;若不能,请说明理由.
吗?若能,求出满足条件的D点的位置;若不能,请说明理由.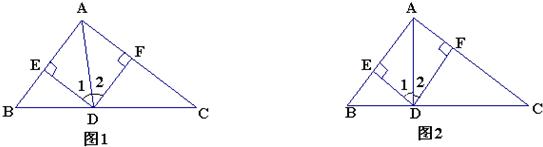
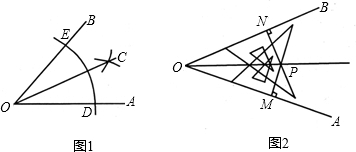
 12、用直尺和圆规作一个角的角平分线示意图如图所示,则说明∠AOC=∠BOC的依据是
12、用直尺和圆规作一个角的角平分线示意图如图所示,则说明∠AOC=∠BOC的依据是湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com