
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1+1 |
| 2+1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5+2 |
| 4+2 |
| 7 |
| 6 |
| 5 |
| 4 |
| 3 |
| 5 |
| 3+5 |
| 5+5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 2 |
| 7+3 |
| 2+3 |
| 7 |
| 2 |
|
2
|
|
3
|
|
4
|
|
|
|
|
2
|
|
|
|
|
3
|
5
|
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2×3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3×4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4×5 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 2 |
| 3 |
观察下列等式:
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④![]() ;
;
……
1.猜想并写出第![]() 个算式: ;
个算式: ;
2.请说明你写出的等式的正确性.
3.把上述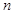 个算式的两边分别相加,会得到下面的求和公式吗?请写出具体的推导过程.
个算式的两边分别相加,会得到下面的求和公式吗?请写出具体的推导过程.
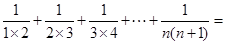 .
.
4.我们规定:分子是1,分母是正整数的分数叫做单位分数.任意一个真分数都可以表示成不同的单位分数的和的形式,且有无数多种表示方法.根据上面得出的两个结论,请将真分数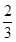 表示成不同的单位分数的和的形式.(写出一种即可)
表示成不同的单位分数的和的形式.(写出一种即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com