
题目列表(包括答案和解析)
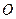 和
和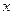 轴上另一点
轴上另一点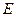 ,顶点
,顶点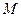 的坐标为
的坐标为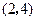 ;矩形
;矩形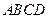 的顶点
的顶点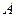 与点
与点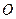 重合,
重合,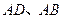 分别在
分别在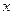 轴、
轴、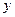 轴上,且
轴上,且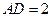 ,
,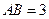 .
.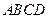 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿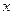 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点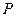 也以相同的速度从点
也以相同的速度从点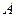 出发向
出发向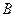 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为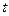 秒(
秒(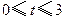 ),直线
),直线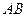 与该抛物线的交点为
与该抛物线的交点为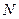 (如图2所示).
(如图2所示).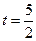 时,判断点
时,判断点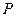 是否在直线
是否在直线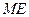 上,并说明理由;
上,并说明理由;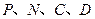 为顶点的多边形面积为
为顶点的多边形面积为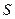 ,试问
,试问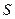 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.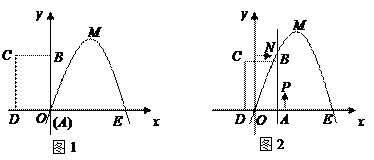
(本小题满分12分)如图1,已知抛物线经过坐标原点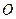 和
和 轴上另一点
轴上另一点 ,顶点
,顶点 的坐标为
的坐标为 ;矩形
;矩形 的顶点
的顶点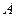 与点
与点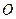 重合,
重合,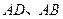 分别在
分别在 轴、
轴、 轴上,且
轴上,且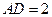 ,
, .
.
(1)求该抛物线所对应的函数关系式;
(2)将矩形 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点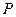 也以相同的速度从点
也以相同的速度从点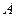 出发向
出发向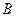 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为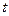 秒(
秒(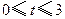 ),直线
),直线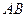 与该抛物线的交点为
与该抛物线的交点为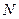 (如图2所示).
(如图2所示).
①当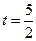 时,判断点
时,判断点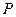 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
②设以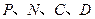 为顶点的多边形面积为
为顶点的多边形面积为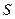 ,试问
,试问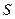 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.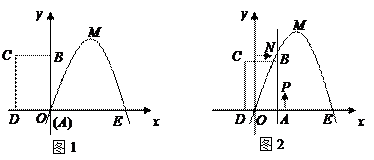
(本小题满分12分)
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.
(1)试问小球通过第二层![]() 位置的概率是多少?
位置的概率是多少?
(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层 位置和第四层
位置和第四层
位置处的概率各是多少?

 位置的概率是多少?
位置的概率是多少?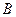 位置和第四层
位置和第四层

(本小题满分12分)
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.
(1)试问小球通过第二层 位置的概率是多少?
位置的概率是多少?
(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层 位置和第四层
位置和第四层
位置处的概率各是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com