
题目列表(包括答案和解析)
如图1,把矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1 cm/s,设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论:
①AD=BE=5 cm;
②当0<t≤5时;y=![]() t2;
t2;
③直线NH的解析式为y=-![]() t+27;
t+27;
④若△ABE与△QBP相似,则t=![]() 秒.
秒.
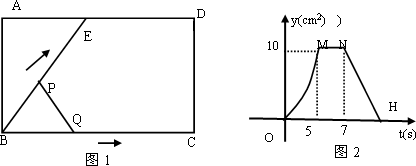
其中正确的结论个数为
A.4
B.3
C.2
D.1
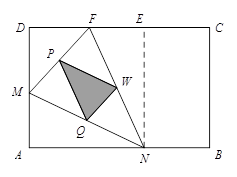
如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
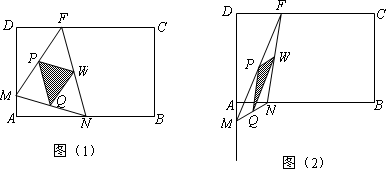
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时,△PQW为直角三角形?当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值.
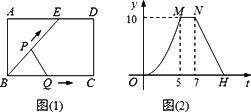
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1 cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=![]() ;③当0<t≤5时,y=
;③当0<t≤5时,y=![]() t2;④当t=
t2;④当t=![]() 秒时,△ABE∽△QBP;其中正确的结论是________(填序号).
秒时,△ABE∽△QBP;其中正确的结论是________(填序号).
如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC
上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、MN、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
1.DM=___▲____, AN=___▲____(用含x的代数式表示)
2.说明△FMN  ∽ △QWP;
∽ △QWP;
3.试问![]() 为何值时,△PQW为直角三角形?
为何值时,△PQW为直角三角形?
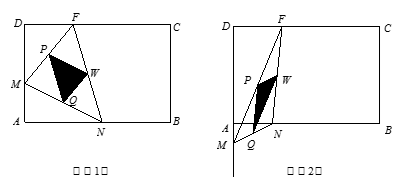
4.问当![]() 为____▲_____时,线段MN最短?
为____▲_____时,线段MN最短?
 ∽ △QWP;
∽ △QWP;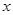 为何值时,△PQW为直角三角形?
为何值时,△PQW为直角三角形? 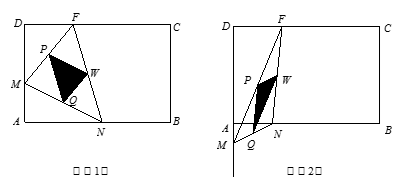
 为____▲_____时,线段MN最短?
为____▲_____时,线段MN最短?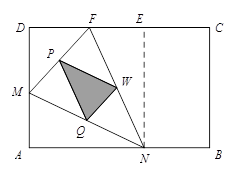
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com