(本题满分12分)一名篮球运动员传球，球沿抛物线y＝－x²+2x+4运行，传球时，球的出手点P的高度为1.8米，一名防守队员正好处在抛物线所在的平面内，他原地竖直起跳的最大高度为3.2米，
问：【小题1】（1）球在下落过程中，防守队员原地竖直起跳后在到达最大高度时刚好将球断掉，那么传球时，两人相距多少米？
【小题2】（2）要使球在运行过程中不断防守队员断掉，且仍按抛物线y＝－x²+2x+4运行，那么两人间的距离应在什么范围内？（结果保留根号）

(本题满分12分) 如图，在平面直角坐标系中，抛物线与x轴交于点A、B

(点A在点B的左侧)，与y轴交于点C(0，4)，顶点为(1，)．

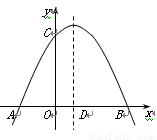
(1)求抛物线的函数解析式；

(2)抛物线的对称轴与x轴交于点D，点P在对称轴上且使△CDP为等腰三角形．请直接写出满足条件的所有点的坐标P；

(3)若点E是线段AB上的一个动点(与点A、B不重合)，连接AC、BC，过点E作EF∥AC交线段BC于点F，连接CE，记△CEF的面积为S，S是否存在最大值？若存在，请求出S的最大值及此时点E的坐标；若不存在，请说明理由．

计算（本题满分12分，每题4分）
(1)   ―1²⁰¹² + (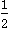)^－1―(3.14－π)⁰ 
（2） (－6xy²)²(―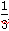 xy + 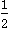 y² ―x²) 
(3) 先化简，再求值：(2m+n)²－(3m－n)²+5m(m－n)，其中m=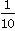，n=．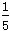

(本题满分12分）春节期间，七（1）班的李平、王丽等同学随家长一同到某公园游玩，下面是购买门票时，李平与他爸爸的对话（如图），试根据图中的信息，解答下列问题：

⑴李平他们一共去了几个成人，几个学生？
⑵请你帮助算一算，用哪种方式购票更省钱？说明理由。
⑶购完票后，李平发现七⑵班的张明等8名同学和他们的12名家长共20人也来购票，请你为他们设计出最省的购票方案，并求出此时的购票费用.