
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
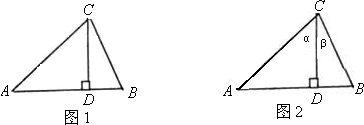
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.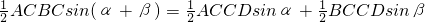 ,即
,即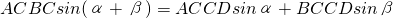 ②.
②.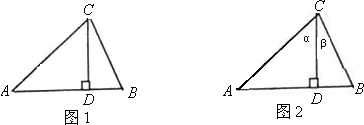
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.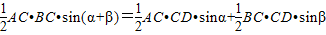 ,即
,即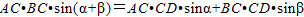 ②.
②.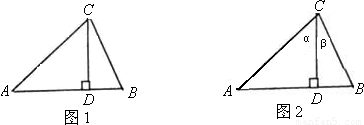
 在初中阶段我们已经学习了很多数学知识,能够解决一些实际问题.请用你已经学过的数学知识解决下列问题.如图表示的是一条河流的某一段,两岸是平行的,河的两岸不能到达,现在要测出河宽.请你结合图形写出测河宽的过程,并用数据或字母表示结果.
在初中阶段我们已经学习了很多数学知识,能够解决一些实际问题.请用你已经学过的数学知识解决下列问题.如图表示的是一条河流的某一段,两岸是平行的,河的两岸不能到达,现在要测出河宽.请你结合图形写出测河宽的过程,并用数据或字母表示结果.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com