
题目列表(包括答案和解析)
给出下列四个命题:
①若直线l∥平面α,l∥平面β,则α∥β;
②各侧面都是正方形的棱柱一定是正棱柱;
③一个二面角的两个半平面所在的平面分别垂直于另一个二面角的两个半平面所在的平面,则这两个二面角的平面角相等或互为补角;
④过空间任意一点P一定可以作一个和两条异面直线(点P不再此两条异面直线上)都平行的平面.
其中不正确的命题的个数有
1
2
3
4
给出下列四个命题:
①若直线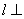 平面
平面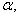
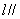 平面
平面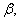 则
则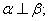
②若平面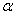 内有不共线的三点到平面
内有不共线的三点到平面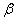 的距离相等,则
的距离相等,则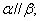
③若一个二面角的两个半平面所在的平面分别垂直于另一个二面角的两个半平面所在的平面,则这两个二面角的平面角互为补角;
④过空间中任意一点一定可以作一个和两条异面直线都平行的平面.
其中正确命题的个数有( )
A.1 B.2 C.3 D.4
 |
| BC |
 |
| BD |

以下三个命题中,正确的命题有
[ ]
①一个二面角的平面角只有椄?/P>
②二面角的棱垂直于这个二面角的平面角所在的平面
③分别在二面角的两个半平面内,且垂直于棱的
两直线所成的角等于二面角的大小
以下三个命题中,正确的命题有
[
]①一个二面角的平面角只有锐角
②二面角的棱垂直于这个二面角的平面角所在的平面
③分别在二面角的两个半平面内,且垂直于棱的两直线所成的角等于二面角的大小
|
A ,0个 |
B .1个 |
C .2个 |
D .3个 |
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
B
B
C
D
C
A
C
D
A
二、填空题:
13. 试题.files/image175.gif) 14.
14. 试题.files/image177.gif) 15. 2个 16.
15. 2个 16. 试题.files/image179.gif)
试题.files/image181.gif)
三、解答题:
17.解:(1)试题.files/image183.gif)
试题.files/image185.gif) ……………………3分
……………………3分
又 试题.files/image187.gif)
试题.files/image189.gif) 即
即 试题.files/image191.gif)
试题.files/image193.gif)
试题.files/image195.gif) …………………5分
…………………5分
(2)试题.files/image197.gif)
试题.files/image199.gif)
又 试题.files/image201.gif)
试题.files/image203.gif) 是
是试题.files/image205.gif) 的充分条件
的充分条件 试题.files/image207.gif) 解得
解得 试题.files/image209.gif) ………12分
………12分
18.由题意知,在甲盒中放一球概率为试题.files/image022.gif) 时,在乙盒中放一球的概率为
时,在乙盒中放一球的概率为试题.files/image212.gif) …2分
…2分
①当试题.files/image214.gif) 时,
时,试题.files/image216.gif) ,
,试题.files/image218.gif) 的概率为
的概率为试题.files/image220.gif) ………4分
………4分
②当试题.files/image222.gif) 时,
时,试题.files/image224.gif) ,又
,又试题.files/image226.gif) ,所以
,所以试题.files/image132.gif) 的可能取值为0,2,4
的可能取值为0,2,4
(?)当试题.files/image229.gif) 时,有
时,有试题.files/image231.gif) ,
,试题.files/image233.gif) ,它的概率为
,它的概率为试题.files/image235.gif) ………6分
………6分
(?)当试题.files/image237.gif) 时,有
时,有试题.files/image216.gif) ,
,试题.files/image240.gif) 或
或试题.files/image242.gif) ,
,试题.files/image244.gif)
它的概率为试题.files/image246.gif)
(?)当试题.files/image248.gif) 时,有
时,有试题.files/image250.gif) 或
或试题.files/image252.gif)
它的概率为试题.files/image254.gif)
故试题.files/image132.gif) 的分布列为
的分布列为
试题.files/image132.gif)
0
2
4
P
试题.files/image258.gif)
试题.files/image260.gif)
试题.files/image262.gif)
试题.files/image264.gif) 的数学期望
的数学期望试题.files/image266.gif) …………12分
…………12分
19.解:(1) 连接试题.files/image268.gif) 交
交试题.files/image270.gif) 于点E,连接DE,
于点E,连接DE,试题.files/image272.gif) ,
,
试题.files/image274.gif) 四边形
四边形试题.files/image276.gif) 为矩形,
为矩形,试题.files/image274.gif) 点E为
点E为试题.files/image268.gif) 的中点,
的中点,
试题.files/image274.gif)
试题.files/image281.gif)
试题.files/image274.gif)
试题.files/image284.gif) 平面
平面试题.files/image286.gif) ……………6分
……………6分
(2)作试题.files/image288.gif) 于F,连接EF
于F,连接EF
试题.files/image290.gif) ,D为AB中点,
,D为AB中点,试题.files/image292.gif) ,
,试题.files/image294.gif)
试题.files/image296.gif)
试题.files/image298.gif) ,
, 试题.files/image274.gif) EF为BE在平面
EF为BE在平面试题.files/image301.gif) 内的射影
内的射影
又试题.files/image303.gif) 为二面角
为二面角试题.files/image305.gif) 的平面角.
的平面角.
设试题.files/image307.gif)
试题.files/image309.gif)
试题.files/image311.gif)
又试题.files/image313.gif) 二面角
二面角试题.files/image305.gif) 的余弦值
的余弦值试题.files/image316.gif) ………12分
………12分
20.(1)据题意的
试题.files/image318.gif) ………4分
………4分
试题.files/image320.gif) ………5分
………5分
(2)由(1)得:当试题.files/image322.gif) 时,
时,试题.files/image324.gif)
试题.files/image326.gif)
当试题.files/image328.gif) 时,
时,试题.files/image330.gif) ,
,试题.files/image332.gif) 为增函数
为增函数
当试题.files/image334.gif) 时,
时,试题.files/image336.gif) 为减函数
为减函数
试题.files/image274.gif) 当
当试题.files/image339.gif) 时,
时,试题.files/image341.gif) …………………………8分
…………………………8分
当试题.files/image343.gif) 时,
时,试题.files/image345.gif)
当试题.files/image347.gif) 时,
时,试题.files/image349.gif)
当试题.files/image351.gif) 时,
时,试题.files/image353.gif) …………………………10分
…………………………10分
综上知:当试题.files/image339.gif) 时,总利润最大,最大值为195 ………………12分
时,总利润最大,最大值为195 ………………12分
21.解:(1)由椭圆定义可得试题.files/image356.gif) ,由
,由试题.files/image358.gif) 可得
可得
试题.files/image360.gif) ,而
,而试题.files/image362.gif)
解得 试题.files/image364.gif) ……………………4分
……………………4分
(2)由试题.files/image366.gif) ,得
,得试题.files/image368.gif) ,
,
试题.files/image370.gif)
解得试题.files/image372.gif) 或
或试题.files/image374.gif) (舍去)
(舍去) 试题.files/image376.gif) 此时
此时试题.files/image378.gif)
当且仅当试题.files/image380.gif) 时,
时,试题.files/image382.gif) 得最小值
得最小值试题.files/image384.gif) ,
,
此时椭圆方程为试题.files/image386.gif) ………………………………………8分
………………………………………8分
(3)由试题.files/image160.gif) 知点Q是AB的中点
知点Q是AB的中点
设A,B两点的坐标分别为试题.files/image389.gif) ,中点Q的坐标为
,中点Q的坐标为试题.files/image391.gif)
则试题.files/image393.gif) ,两式相减得
,两式相减得试题.files/image395.gif)
试题.files/image397.gif)
试题.files/image274.gif) AB的中点Q的轨迹为直线
AB的中点Q的轨迹为直线试题.files/image400.gif) ①
①
且在椭圆内的部分
又由试题.files/image162.gif) 可知
可知试题.files/image403.gif) ,所以直线NQ的斜率为
,所以直线NQ的斜率为试题.files/image405.gif) ,
,
方程为试题.files/image407.gif) ②
②
①②两式联立可求得点Q的坐标为试题.files/image409.gif)
试题.files/image201.gif) 点Q必在椭圆内
点Q必在椭圆内 试题.files/image412.gif) 解得
解得试题.files/image414.gif)
又试题.files/image416.gif)
试题.files/image418.gif) …………………………………12分
…………………………………12分
22.解:(1)由试题.files/image420.gif) ,得
,得试题.files/image422.gif)
令试题.files/image424.gif) ,有
,有试题.files/image426.gif)
试题.files/image428.gif)
试题.files/image430.gif)
又试题.files/image432.gif)
试题.files/image434.gif)
试题.files/image436.gif)
(2)证明:试题.files/image438.gif)
试题.files/image440.gif)
试题.files/image442.gif) 为递减数列
为递减数列
当试题.files/image444.gif) 时,
时,试题.files/image014.gif) 取最大值
取最大值
试题.files/image447.gif)
由(1)中知试题.files/image449.gif)
试题.files/image451.gif)
综上可知试题.files/image167.gif)
(3)试题.files/image454.gif)
欲证:试题.files/image173.gif) 即证
即证试题.files/image457.gif)
即试题.files/image459.gif) ,构造函数
,构造函数试题.files/image461.gif)
试题.files/image463.gif) 当
当试题.files/image465.gif) 时,
时,试题.files/image467.gif)
试题.files/image274.gif) 函数
函数试题.files/image332.gif) 在
在试题.files/image471.gif) 内递减
内递减
试题.files/image473.gif) 在
在试题.files/image475.gif) 内的最大值为
内的最大值为试题.files/image477.gif)
试题.files/image274.gif) 当
当试题.files/image106.gif) 时,
时,试题.files/image481.gif)
又试题.files/image483.gif)
试题.files/image485.gif)
试题.files/image274.gif) 不等式
不等式试题.files/image173.gif) 成立
成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com