
题目列表(包括答案和解析)
 Q,过Q作QR⊥AC于R,再过R作RS⊥AB于S.设AP=x,AS=y.
Q,过Q作QR⊥AC于R,再过R作RS⊥AB于S.设AP=x,AS=y.| 1 | 4 |
|
|
(9分) 甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留半小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.
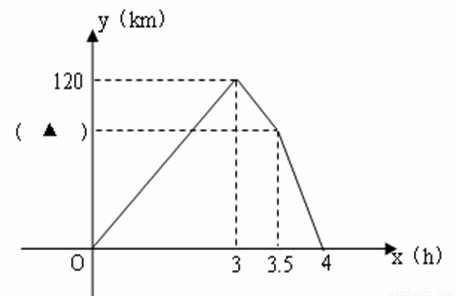
(1)将图中( )填上适当的值,并求甲车从A到B的速度.
(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式,并写出自变量取值范围.
(3)求出甲车返回时行驶速度及AB两地的距离.
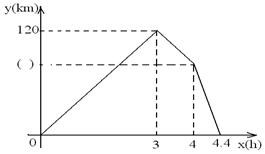
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.
1.将图中( )填上适当的值,并求甲车从A到B的速度.
2.求从甲车返回到与乙车相遇过程中y与x的函数关系式,并写出自变量取值范围.
3.求出甲车返回时行驶速度及AB两地的距离.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com