（1）已知正方形ABCD ，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，求证EG = FH”（如图1）；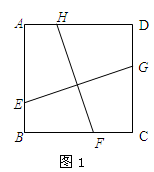

（2）如果把条件中的“正方形”改为“长方形”，并设AB =2，BC =3（如图2），试探究EG、FH之间有怎样的数量关系，并证明你的结论；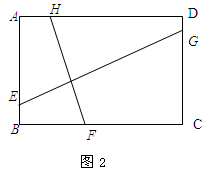

（3）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为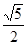（如图3），试求EG的长度。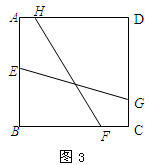

已知：△ABD和△CBD关于直线BD对称(点A的对称点是点C)，点E、F分别是线段BC和线段BD上的点，且点F在线段EC的垂直平分线上，连接AF、AE，AE交BD于点G．

（1）如图l，求证：∠EAF=∠ABD；
（2）如图2，当AB=AD时，M是线段AG上一点，连接BM、ED、MF，MF的延长线交ED于点N，∠MBF= ∠BAF，AF=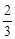AD，试探究线段FM和FN之间的数量关系，并证明你的结论．

如图15，在△ABC和△PQD中，AC = k BC，DP = k DQ，∠C =∠PDQ，D、E分别是AB、AC的中点，点P在直线BC上，连结EQ交PC于点H．猜想线段EH与AC的数量关系，并证明你的猜想．

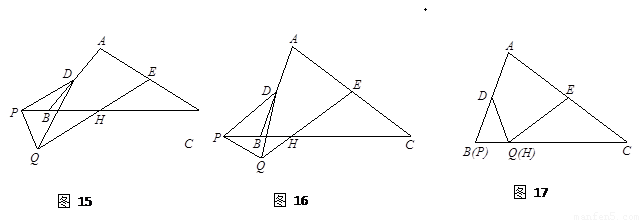
如图15，在△ABC和△PQD中，AC =" k" BC，DP =" k" DQ，∠C =∠PDQ，D、E分别是AB、AC的中点，点P在直线BC上，连结EQ交PC于点H．猜想线段EH与AC的数量关系，并证明你的猜想．