
题目列表(包括答案和解析)
(本小题满分13分)随着石油资源的日益紧缺,我国决定建立自己的石油储备基地,
已知某石油储备基地原储有石油![]() 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出![]() 吨,设
吨,设![]() 为正式运营后第
为正式运营后第![]() 年年底的石油储量.(Ⅰ)求
年年底的石油储量.(Ⅰ)求![]() 、
、![]() 、
、![]() ; (Ⅱ)猜测出
; (Ⅱ)猜测出![]() 的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于
的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于![]() 吨,如果
吨,如果![]() 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:![]() ,
,![]() )
)
(本小题满分13分)
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程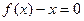 有实数根;②函数
有实数根;②函数 的导数
的导数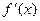 满足
满足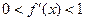 ”.
”.
(1)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)若集合M中的元素具有下面的性质:“若 的定义域为D,则对于任意
的定义域为D,则对于任意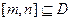 ,都存在
,都存在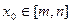 ,使得等式
,使得等式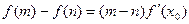 成立”,
成立”, 试用这一性质证明:方程
试用这一性质证明:方程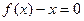 只有一个实数根;
只有一个实数根;
(3)设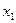 是方程
是方程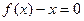 的实
的实 数根,求证:对于
数根,求证:对于 定义域中的任意的
定义域中的任意的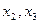 ,当
,当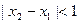 且
且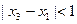 时,
时,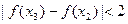 .
.
(本小题满分13分)
设 是数列
是数列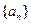 (
(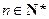 )的前
)的前 项和,
项和, ,且
,且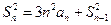 ,
, ,
, .
.
(I)证明:数列 (
(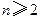 )是常数数列;
)是常数数列;
(II)试找出一个奇数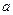 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列 (
(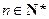 )中的所有项都是数列
)中的所有项都是数列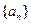 中的项,并指出
中的项,并指出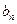 是数列
是数列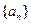 中的第几项.
中的第几项.
(本小题满分13分)
已知,在水平平面 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)当 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求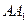 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面 与平面
与平面 所成的角为
所成的角为 ,
, 长方体
长方体 的最高点离平面
的最高点离平面 的距离为
的距离为 ,请直接写出
,请直接写出 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.
(本小题满分13分)已知函数 (其中
(其中 且
且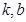 为常数)的图像经过点A
为常数)的图像经过点A 、B
、B .
. 是函数
是函数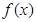 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点.
(1) 求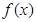 的解析式;
的解析式;
(2) 设 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列 满足
满足 ,记
,记 的前
的前 项和为
项和为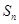 ,证明:
,证明: 。
。
一. 选择题
1A 2D 3B 4D 5C 6A 7B 8C 9B 10A 11D 12C
二. 13: 含详解.files/image264.gif) 14: 1 15:
14: 1 15: 含详解.files/image266.gif) 16:
16:
含详解.files/image268.gif)
(1).复数 含详解.files/image020.gif) ( )
( )
A.2 B.-2
C. 含详解.files/image022.gif) D.
D. 含详解.files/image024.gif)
解:含详解.files/image270.gif)
含详解.files/image272.gif) ,选A。
,选A。
(2).集合含详解.files/image026.gif) ,
,含详解.files/image028.gif) 则下列结论正确的是(
)
则下列结论正确的是(
)
A.含详解.files/image030.gif) B.
B.
含详解.files/image032.gif)
C.含详解.files/image034.gif) D.
D. 含详解.files/image036.gif)
解: 含详解.files/image274.gif) ,
,含详解.files/image276.gif) ,又
,又含详解.files/image278.gif)
∴ 含详解.files/image280.gif) ,选D。
,选D。
(3).在平行四边形ABCD中,AC为一条对角线,若含详解.files/image038.gif) ,
,含详解.files/image040.gif) ,则
,则含详解.files/image042.gif) ( )
( )
A. (-2,-4) B.(-3,-5) C.(3,5) D.(2,4)
解:因为含详解.files/image282.gif) ,选B。
,选B。
(4).已知含详解.files/image044.gif) 是因为
是因为含详解.files/image282.gif) ,选B。。
,选B。。
两条不同直线,含详解.files/image046.gif) 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A.含详解.files/image048.gif) B.
B.含详解.files/image050.gif)
C.含详解.files/image052.gif) D.
D.含详解.files/image054.gif)
解: 含详解.files/image044.gif) 均为直线,其中
均为直线,其中含详解.files/image044.gif) 平行
平行含详解.files/image285.gif) ,
,含详解.files/image044.gif) 可以相交也可以异面,故A不正确;
可以相交也可以异面,故A不正确;
m含详解.files/image287.gif)
含详解.files/image285.gif) ,n⊥α则同垂直于一个平面的两条直线平行;选D。
,n⊥α则同垂直于一个平面的两条直线平行;选D。
(5).将函数含详解.files/image056.gif) 的图象按向量
的图象按向量含详解.files/image058.gif) 平移后所得的图象关于点
平移后所得的图象关于点含详解.files/image060.gif) 中心对称,则向量
中心对称,则向量含详解.files/image058.gif) 的坐标可能为( )
的坐标可能为( )
A.含详解.files/image060.gif) B.
B.含详解.files/image062.gif) C.
C.含详解.files/image064.gif) D.
D.含详解.files/image066.gif)
解:设平移向量含详解.files/image290.gif) ,则函数按向量平移后的表达式为
,则函数按向量平移后的表达式为
含详解.files/image292.gif) ,因为图象关于点
,因为图象关于点含详解.files/image294.gif) 中心对称,
中心对称,
故含详解.files/image296.gif) 代入得:
代入得: 含详解.files/image298.gif) ,
,含详解.files/image300.gif) ,
,
k=0得:含详解.files/image302.gif) ,选C。本题也可以从选择支出发,逐个排除也可。
,选C。本题也可以从选择支出发,逐个排除也可。
(6).设含详解.files/image068.gif) 则
则含详解.files/image070.gif) 中奇数的个数为( )
中奇数的个数为( )
A.2 B.3 C.4 D.5
解:由题知含详解.files/image304.gif) ,逐个验证知
,逐个验证知含详解.files/image306.gif) ,其它为偶数,选A。
,其它为偶数,选A。
(7).含详解.files/image072.gif) 是方程
是方程含详解.files/image074.gif) 至少有一个负数根的( )
至少有一个负数根的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
解:当含详解.files/image308.gif) ,得a<1时方程有根。a<0时,
,得a<1时方程有根。a<0时,含详解.files/image310.gif) ,方程有负根,又a=1时,方程根为
,方程有负根,又a=1时,方程根为含详解.files/image312.gif) ,所以选B
,所以选B
(8).若过点含详解.files/image076.gif) 的直线
的直线含详解.files/image078.gif) 与曲线
与曲线含详解.files/image080.gif) 有公共点,则直线
有公共点,则直线含详解.files/image078.gif) 的斜率的取值范围为( ) A.
的斜率的取值范围为( ) A.含详解.files/image082.gif) B.
B.含详解.files/image084.gif) C.
C.含详解.files/image086.gif) D.
D.含详解.files/image088.gif)
解:设直线方程为含详解.files/image314.gif) ,即
,即含详解.files/image316.gif) ,直线
,直线含详解.files/image078.gif) 与曲线
与曲线含详解.files/image080.gif) 有公共点,
有公共点,
含详解.files/image318.gif) 圆心到直线的距离小于等于半径
圆心到直线的距离小于等于半径
含详解.files/image320.gif) ,
,
得含详解.files/image322.gif) ,选择C
,选择C
另外,数形结合画出图形也可以判断C正确。
(9).在同一平面直角坐标系中,函数含详解.files/image090.gif) 的图象与
的图象与含详解.files/image092.gif) 的图象关于直线
的图象关于直线含详解.files/image094.gif) 对称。而函数
对称。而函数含详解.files/image096.gif) 的图象与
的图象与含详解.files/image090.gif) 的图象关于
的图象关于含详解.files/image098.gif) 轴对称,若
轴对称,若含详解.files/image100.gif) ,则
,则含详解.files/image102.gif) 的值是( )
的值是( )
A.含详解.files/image104.gif) B.
B.含详解.files/image106.gif) C.
C.含详解.files/image108.gif) D.
D.含详解.files/image110.gif)
解:由题知含详解.files/image324.gif) 则
则含详解.files/image326.gif) ,
,含详解.files/image328.gif) 选D。
选D。
(10).设两个正态分布含详解.files/image112.gif) 和
和含详解.files/image114.gif) 的密度函数图像如图所示。则有( )
的密度函数图像如图所示。则有( )
含详解.files/image116.jpg) A.
A.含详解.files/image118.gif)
B.含详解.files/image120.gif)
C.含详解.files/image122.gif)
D.含详解.files/image124.gif)
解:根据正态分布含详解.files/image330.gif) 函数的性质:正态分布曲线是一条关于
函数的性质:正态分布曲线是一条关于含详解.files/image332.gif) 对称,在
对称,在含详解.files/image332.gif) 处取得最大值的连续钟形曲线;
处取得最大值的连续钟形曲线;含详解.files/image335.gif) 越大,曲线的最高点越底且弯曲较平缓;反过来,
越大,曲线的最高点越底且弯曲较平缓;反过来,含详解.files/image337.gif) 越小,曲线的最高点越高且弯曲较陡峭,选A。
越小,曲线的最高点越高且弯曲较陡峭,选A。
(11).若函数含详解.files/image126.gif) 分别是
分别是含详解.files/image008.gif) 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足含详解.files/image129.gif) ,则有( )
,则有( )
A.含详解.files/image131.gif) B.
B.含详解.files/image133.gif)
C.含详解.files/image135.gif) D.
D.含详解.files/image137.gif)
解: 用含详解.files/image339.gif) 代换x得:
代换x得: 含详解.files/image341.gif)
含详解.files/image343.gif) ,
,
解得:含详解.files/image345.gif) ,而
,而含详解.files/image185.gif) 单调递增且大于等于0,
单调递增且大于等于0,含详解.files/image348.gif) ,选D。
,选D。
(12)12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是( )
A.含详解.files/image139.gif) B.
B.含详解.files/image141.gif) C.
C.含详解.files/image143.gif) D.
D.含详解.files/image145.gif)
解:从后排8人中选2人共含详解.files/image350.gif) 种选法,这2人插入前排4人中且保证前排人的顺序不变,则先从4人中的5个空挡插入一人,有5种插法;余下的一人则要插入前排5人的空挡,有6种插法,故为
种选法,这2人插入前排4人中且保证前排人的顺序不变,则先从4人中的5个空挡插入一人,有5种插法;余下的一人则要插入前排5人的空挡,有6种插法,故为含详解.files/image352.gif) ;综上知选C。
;综上知选C。
(13).函数含详解.files/image147.gif) 的定义域为
.
的定义域为
.
解:由题知:含详解.files/image354.gif) ;解得:x≥3.
;解得:x≥3.
(14)在数列含详解.files/image149.gif) 在中,
在中,含详解.files/image151.gif) ,
,含详解.files/image153.gif) ,
,含详解.files/image155.gif) ,其中
,其中含详解.files/image157.gif) 为常数,则
为常数,则含详解.files/image159.gif) 的值是
的值是
解: ∵含详解.files/image356.gif) ∴
∴含详解.files/image358.gif) 从而
从而含详解.files/image360.gif) 。
。
∴a=2,含详解.files/image362.gif) ,则
,则含详解.files/image364.gif)
(15)若含详解.files/image161.gif) 为不等式组
为不等式组含详解.files/image163.gif) 表示的平面区域,则当
表示的平面区域,则当含详解.files/image165.gif) 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线含详解.files/image167.gif) 扫过
扫过含详解.files/image161.gif) 中的那部分区域的面积为
中的那部分区域的面积为
解:如图知含详解.files/image366.gif) 是斜边为3 的等腰直角三角形,
是斜边为3 的等腰直角三角形,含详解.files/image368.gif) 是直角边为1等腰直角三角形,区域的面积
是直角边为1等腰直角三角形,区域的面积含详解.files/image370.gif)
含详解.files/image377.gif) |
(16)已知含详解.files/image169.gif) 在同一个球面上,
在同一个球面上,含详解.files/image171.gif)
含详解.files/image173.gif) 若
若含详解.files/image175.gif)
含详解.files/image177.gif)
含详解.files/image179.gif) ,则
,则含详解.files/image181.gif) 两点间的球面距离是
两点间的球面距离是
解: 如图,易得含详解.files/image380.gif) ,
,含详解.files/image382.gif) ,
,含详解.files/image384.gif) ,则此球内接长方体三条棱长为AB、BC、CD(CD的对边与CD等长),从而球外接圆的直径为
,则此球内接长方体三条棱长为AB、BC、CD(CD的对边与CD等长),从而球外接圆的直径为含详解.files/image386.gif) ,R=4则BC与球心构成的大圆如图,因为△OBC为正三角形,则B,C两点间的球面距离是
,R=4则BC与球心构成的大圆如图,因为△OBC为正三角形,则B,C两点间的球面距离是含详解.files/image268.gif) 。
。
三. 解答题
17解:(1)含详解.files/image389.gif)
含详解.files/image391.gif)
含详解.files/image393.gif)
含详解.files/image395.gif)
含详解.files/image397.gif)
含详解.files/image399.gif)
由含详解.files/image401.gif)
含详解.files/image403.gif) 函数图象的对称轴方程为
函数图象的对称轴方程为 含详解.files/image405.gif)
(2)含详解.files/image407.gif)
因为含详解.files/image409.gif) 在区间
在区间含详解.files/image411.gif) 上单调递增,在区间
上单调递增,在区间含详解.files/image413.gif) 上单调递减,
上单调递减,
所以 当含详解.files/image415.gif) 时,
时,含详解.files/image185.gif) 去最大值 1
去最大值 1
又 含详解.files/image418.gif) ,当
,当含详解.files/image420.gif) 时,
时,含详解.files/image185.gif) 取最小值
取最小值含详解.files/image423.gif)
所以 函数 含详解.files/image185.gif) 在区间
在区间含详解.files/image187.gif) 上的值域为
上的值域为含详解.files/image427.gif)
含详解.files/image429.gif) 18 方法一(综合法)
18 方法一(综合法)
(1)取OB中点E,连接ME,NE
含详解.files/image431.gif)
又含详解.files/image433.gif)
含详解.files/image435.gif)
(2)含详解.files/image437.gif)
含详解.files/image439.gif) 为异面直线
为异面直线含详解.files/image257.gif) 与
与含详解.files/image442.gif) 所成的角(或其补角)
所成的角(或其补角)
作含详解.files/image444.gif) 连接
连接含详解.files/image446.gif)
含详解.files/image448.gif)
含详解.files/image450.gif)
含详解.files/image452.gif) ,
,含详解.files/image454.gif)
所以 含详解.files/image257.gif) 与
与含详解.files/image442.gif) 所成角的大小为
所成角的大小为含详解.files/image456.gif)
(3)含详解.files/image458.gif) 点A和点B到平面OCD的距离相等,连接OP,过点A作
点A和点B到平面OCD的距离相等,连接OP,过点A作
含详解.files/image460.gif) 于点Q,
于点Q,含详解.files/image462.gif)
又 含详解.files/image464.gif) ,线段AQ的长就是点A到平面OCD的距离
,线段AQ的长就是点A到平面OCD的距离
含详解.files/image466.gif) ,
,含详解.files/image468.gif)
含详解.files/image470.gif) ,所以点B到平面OCD的距离为
,所以点B到平面OCD的距离为含详解.files/image472.gif)
方法二(向量法)
作含详解.files/image474.gif) 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为含详解.files/image476.gif) 轴建立坐标系
轴建立坐标系
含详解.files/image478.gif) ,
,
(1)含详解.files/image480.gif)
含详解.files/image482.gif) 设平面OCD的法向量为
设平面OCD的法向量为含详解.files/image484.gif) ,则
,则含详解.files/image486.gif)
即 含详解.files/image488.gif)
取含详解.files/image490.gif) ,解得
,解得含详解.files/image492.gif)
含详解.files/image494.gif)
含详解.files/image435.gif)
(2)设含详解.files/image257.gif) 与
与含详解.files/image442.gif) 所成的角为
所成的角为含详解.files/image496.gif) ,
,含详解.files/image498.gif)
含详解.files/image500.gif) ,
, 含详解.files/image257.gif) 与
与含详解.files/image442.gif) 所成角的大小为
所成角的大小为含详解.files/image456.gif)
(3)设点B到平面OCD的交流为含详解.files/image502.gif) ,则
,则含详解.files/image502.gif) 为
为含详解.files/image505.gif) 在向量
在向量含详解.files/image492.gif) 上的投影的绝对值,
上的投影的绝对值,
由 含详解.files/image507.gif) , 得
, 得含详解.files/image509.gif) .所以点B到平面OCD的距离为
.所以点B到平面OCD的距离为含详解.files/image472.gif)
19 (1)由含详解.files/image511.gif) 得
得含详解.files/image513.gif) ,从而
,从而含详解.files/image515.gif)
含详解.files/image213.gif) 的分布列为
的分布列为
含详解.files/image213.gif)
0
1
2
3
4
5
6
含详解.files/image518.gif)
含详解.files/image520.gif)
含详解.files/image522.gif)
含详解.files/image524.gif)
含详解.files/image526.gif)
含详解.files/image524.gif)
含详解.files/image522.gif)
含详解.files/image520.gif)
(2)记”需要补种沙柳”为事件A, 则含详解.files/image </div>
</div>
<div class=)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com