
题目列表(包括答案和解析)
正负电子对撞机的最后部分的简化示意图如图甲所示(俯视图),位于水平面内的粗实线所示的圆环形真空管道是正、负电子做圆运动的“容器”,经过加速器加速后的正、负电子被分别引入该管道时,具有相等的速率v,它们沿着管道向相反的方向运动.在管道内控制它们转弯的是一系列圆形电磁铁,即图中的A1、A2、A3……An共有n个,均匀分布在整个圆环上,每个电磁铁内的磁场都是磁感应强度相同的匀强磁场,并且方向竖直向下,磁场区域的直径为d,改变电磁铁内电流的大小,就可改变磁场的磁感应强度,从而改变电子偏转的角度.经过精确的调整,首先实现电子在环形管道中沿图甲中粗虚线所示的轨迹运动,这时电子经过每个电磁场区域时射入点和射出点都是电磁场区域的同一条直径的两端,如图乙所示.这就为进一步实现正、负电子的对撞作好了准备.

(1)试确定正、负电子在管道内各是沿什么方向旋转的;
(2)已知正、负电子的质量都是m,所带电荷都是元电荷e,重力可不计,求电磁铁内匀强磁场的磁感应强度B的大小.
 ,求:
,求: 点进入磁场时的速度大小;
点进入磁场时的速度大小; 处于不同的位置(原点
处于不同的位置(原点 始终在磁场区域的边界上),电子从磁场区域射出时的偏转角也将不同。求 电子从磁场区域射出时偏转角可达到的最大值。
始终在磁场区域的边界上),电子从磁场区域射出时的偏转角也将不同。求 电子从磁场区域射出时偏转角可达到的最大值。
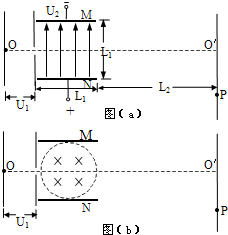 如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的电压为U2,两极板间距离与板长相等,均为L1,板的右端到荧光屏的距离为L2,已知U1=200V,U2=300V,L1=6cm,L2=21cm,电子的比荷e/m=1.8×1011C/kg.求:
如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的电压为U2,两极板间距离与板长相等,均为L1,板的右端到荧光屏的距离为L2,已知U1=200V,U2=300V,L1=6cm,L2=21cm,电子的比荷e/m=1.8×1011C/kg.求: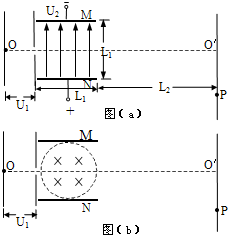
如图所示,匀强磁场分布在0≤x≤2L且以直线PQ为下边界的区域内,∠OPQ=30o。y≤0的区域内存在着沿y轴正向的匀强电场。一质量为m、电荷量为q的带正电粒子(不计粒子重力)从电场中一点M(-![]() L,-
L,-![]() )以初速度v0沿x轴正方向射出后,恰好经过坐标原点O进入第I象限,最后刚好不能从磁场的右边界飞出。求:
)以初速度v0沿x轴正方向射出后,恰好经过坐标原点O进入第I象限,最后刚好不能从磁场的右边界飞出。求:
(1)匀强电场的电场强度的大小E;
(2)匀强磁场的磁感应强度的大小B;
(3)粒子从M点出发到离开磁场过程中所用的时间。
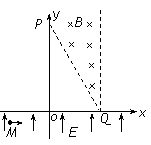
一、选择题
1.C 2.D 3.A 4.D 5.C 6.C 7.D 8.C 9.D 10.D
11.A 12.B 13.B二、选择题
14.D 15.D 16.AC 17.AD 18.D 19.C 20.CD 21.A
三、选择题
22.(18分)
(1)(每空3分)24.12~24.14 0.514~0.517
(2)(每空4分)偏小; 理科综合.files/image226.gif)
(3)(每空4分)图略
(4)A.轨迹图略(任意画出理科综合.files/image150.gif) 点不给分)
点不给分)
B.参考方法一:在轨迹上选两个点A、B
如图1,量出理科综合.files/image229.gif) 、
、理科综合.files/image231.gif) 、
、理科综合.files/image233.gif)
推导:理科综合.files/image235.gif)
理科综合.files/image237.gif)
理科综合.files/image239.gif)
导出 理科综合.files/image241.gif)
理科综合.files/image243.jpg)
参考方法二:在轨迹上选三个点A、B、C
如图2,量出理科综合.files/image245.gif) 、
、理科综合.files/image247.gif) 、
、理科综合.files/image249.gif)
推导 理科综合.files/image251.gif)
导出 理科综合.files/image253.gif)
理科综合.files/image255.jpg)
其他方法:根据抛物线方程推导等(略)
23.(15分)解:(1)设最高点
理科综合.files/image257.gif) (2分)
(2分)
最低点理科综合.files/image259.gif) (2分)
(2分)
机械能守恒理科综合.files/image261.gif) (2分)
(2分)
理科综合.files/image263.gif) (2分)
(2分)
理科综合.files/image265.gif) (2分)
(2分)
(2)理科综合.files/image267.gif) (3分)
(3分)
所以理科综合.files/image269.gif) (2分)
(2分)
24.(19分)解:(1)理科综合.files/image182.gif) 作用后,
作用后,理科综合.files/image272.gif) 均做匀加速直线运动
均做匀加速直线运动
理科综合.files/image274.gif)
理科综合.files/image276.gif) (1分)
(1分)
理科综合.files/image278.gif)
理科综合.files/image280.gif) (1分)
(1分)
理科综合.files/image282.gif) (1分)
(1分)
设经理科综合.files/image284.gif) 时间
时间理科综合.files/image168.gif) 、
、理科综合.files/image170.gif) 相遇,相遇时
相遇,相遇时理科综合.files/image288.gif) (1分)
(1分)
理科综合.files/image290.gif) (1分)
(1分)理科综合.files/image292.gif) 解得
解得理科综合.files/image294.gif) (1分)
(1分)
(2)相遇前理科综合.files/image296.gif) (1分)
(1分)
理科综合.files/image298.gif) (1分)
(1分)
理科综合.files/image300.gif) (1分)
(1分)
最终理科综合.files/image272.gif) 相对静止,
相对静止,理科综合.files/image182.gif) 撤去后系统
撤去后系统理科综合.files/image304.gif)
理科综合.files/image306.gif) (1分)
(1分)
理科综合.files/image308.gif)
(3)理科综合.files/image292.gif) (1分)
(1分)
理科综合.files/image311.gif) (1分)
(1分)
理科综合.files/image313.gif) (1分)
(1分) 理科综合.files/image315.gif) (1分)
(1分)
理科综合.files/image317.gif) (1分)
(1分) 理科综合.files/image319.gif) (1分)
(1分)
理科综合.files/image321.gif) (1分)
(1分)
理科综合.files/image323.gif) (1分)
(1分)
理科综合.files/image325.gif) (1分)
(1分)
25.(20分)(1)由理科综合.files/image327.gif) 得
得理科综合.files/image329.gif) (3分)
(3分)
由理科综合.files/image331.gif) (
(理科综合.files/image092.gif) 为电子圆轨道半径) (3分)
为电子圆轨道半径) (3分)
得理科综合.files/image334.gif) (3分)
(3分)
(3分)
理科综合.files/image336.jpg)
(2)由图可知:理科综合.files/image338.gif) (3分)
(3分)
圆轨道对应的弦越长,圆心角越大,即偏转角越大。当弦长为圆形磁场的直径时.电子射出磁场区域时的偏转角最大为理科综合.files/image340.gif) (3分)
(3分)
由图可知:理科综合.files/image342.gif) (2分)
(2分)
26.(15分)(每空3分共15分)A BaCl2 B(NH4)2 SO4
C AgNO3 D NaCO3 E A12(SO4)3
27.(20分)(Ⅰ)(共14分)
(1)18(2分)
(2)CH2O2(2分) HCOOH(2分)
(3)C2 H2O3(2分) OHC―COOH(2分)
(4)CH3COOH(2分) HCOOCH3(2分)
(Ⅱ)(6分)理科综合.files/image344.jpg)
理科综合.files/image346.jpg) (每空2分)
(每空2分)
28.(13分)
(1)A12O3(2分)Fe2O3(2分)
(2)2Al+Fe2O3====Al2O3+2Fe(3分)
(3)Al理科综合.files/image017.gif) +3A1O
+3A1O理科综合.files/image025.gif) +4H2O====4Al<OH>3↓(3分 )
+4H2O====4Al<OH>3↓(3分 )
(4)理科综合.files/image350.gif) (3分)
(3分)
29.(12分)
(1)C→B→D→A→G→H→E→F(4分)
(2)使漏斗下端管口紧靠烧杯内壁;及时关闭活塞,不要让上层液体流出 (2分)
使漏斗内外空气相通,以保证进行(E)操作时漏斗里液体能够流出 (2分)
(3)CCl4与水不互溶l而且溴在CCl4中的溶解度比在水中的大很多(2分)
(4)(A)(C)(2分)
30.(22分)I.(8分)(每空1分)
① 生长素促进植物生长具有双重性,双子叶植物比单子叶植物对生长素敏感
② b a ③ D
Ⅱ.(14分)① 竞争(1分) 种类斗争、寄生、捕食等(3分)
② 食物和栖息场所(2分)
③ 自动调节(1分);
④ 以甲种群植物为食的其他生物也随之减少,甚至灭绝(2分)
⑤ 缺乏有利变异(2分)l
⑥ 样方法(1分);
⑦ 衰退型 增长型(2分)
31.(20分)
(1)基因突变(2分);① 一种氨基酸可以由多个密码子决定(2分);
② 突变发生在基因中的非编码序列(2分)(只答非编码区或内含子中的一个给1分)
(2)解离→漂洗→染色→制片(2分);染色体数(2分)
结果预测和分析:
① A装片细胞中的染色体数与甲装片细胞中的染色体数相等一A植株为品种乙(2分);
② A装片中细胞中染色体数是甲装片细胞中染色体数的两倍一A植株为品种丙(2分);
(3)方法1:用植株A与品种甲的植株杂交,获得F1;再用F1自交;观察F1是否结果实。
方法2:用A植株的花药进行离体培养,获得单倍体;再用单倍体植株杂交;观察单倍体植株是否结果实。(3分)(答出一种方案即可。其他合理答案酌情给分。)
(4)人工合成(或反转录法等)(1分);真核生物的基因含有不表达的内含子(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com