
题目列表(包括答案和解析)
(本小题满分10分)
在某学校组织的一次蓝球定点投蓝训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投三次。某同学在A处的命中率 为0.25,在B处的命中率为
为0.25,在B处的命中率为 .该同学选择先在A处投一球,以后都在B处投,用
.该同学选择先在A处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
|
0.03 |
|
|
|
|
 求
求 的值;
的值;
 求随机变量
求随机变量 的数学期量
的数学期量 ;
;
 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为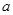 万元,
万元,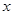 万元,农民得到的补贴为
万元,农民得到的补贴为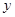 万元,解答以下问题.
万元,解答以下问题.
|
|
A型号 |
B型号 |
|
电视机价值(万元) |
|
|
|
农民获得补贴(万元) |
|
|
(1) 用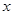 的代数式表示
的代数式表示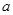
(2) 当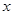 取何值时,
取何值时, 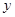 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: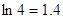 )
)
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为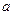 万元,
万元,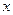 万元,农民得到的补贴为
万元,农民得到的补贴为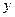 万元,解答以下问题.
万元,解答以下问题.
| | A型号 | B型号 |
| 电视机价值(万元) | 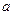 | 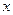 |
| 农民获得补贴(万元) | 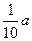 |  |
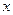 的代数式表示
的代数式表示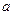
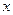 取何值时,
取何值时, 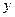 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: )
) 万元,
万元,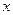 万元,农民得到的补贴为
万元,农民得到的补贴为 万元,解答以下问题.
万元,解答以下问题.| | A型号 | B型号 |
| 电视机价值(万元) |  | 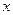 |
| 农民获得补贴(万元) |  |  |
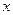 的代数式表示
的代数式表示
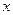 取何值时,
取何值时,  取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: )
)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com