
题目列表(包括答案和解析)
给出下列五个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号,33号,46号同学在样本中,那么样本另一位同学的编号为23;
②一组数据1、2、3、3、4、5的平均数、众数、中位数相同;
③一组数据a、0、1、2、3,若该组数据的平均值为1,则样本标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
 ,
,  ,则
,则 =1;
=1;
⑤如图是根据抽样检测后得出的产品样本净重(单位:克)数据绘制的频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克,并且小于104克的产品的个数是90.
其中真命题为:
| A.①②④ | B.②④⑤ | C.②③④ | D.③④⑤ |

 ,
,  ,则
,则 =1;
=1;
| A.①②④ | B.②④⑤ | C.②③④ | D.③④⑤ |
给出下列五个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号、33号、46号同学在样本中,那么样本中另一位同学的编号为23;
②一组数据1,2,3,3,4,5的平均数、众数、中位数都相同;
③一组数据为 ,0,1,2,3,若该组数据的平均值为1,则样本标准差为2;
,0,1,2,3,若该组数据的平均值为1,则样本标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为 中,
中, 则
则 ;
;
⑤如图是根据抽样检测后得出的产品样本净重(单位:克)数据绘制的频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是90.

其中真命题为( )
A.①②④ B.②④⑤ C.②③④ D.③④⑤
给出下列五个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号、33号、46号同学在样本中,那么样本中另一位同学的编号为23;
②一组数据1,2,3,3,4,5的平均数、众数、中位数都相同;
③一组数据为 ,0,1,2,3,若该组数据的平均值为1,则样本标准差为2;
,0,1,2,3,若该组数据的平均值为1,则样本标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为 中,
中, 则
则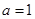 ;
;
⑤如图是根据抽样检测后得出的产品样本净重(单位:克)数据绘制的频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是90.
其中真命题为( )
| A.①②④ | B.②④⑤ | C.②③④ | D.③④⑤ |
| ? |
| y |
| . |
| x |
| . |
| y |
| A.①②④ | B.②④⑤ | C.②③④ | D.③④⑤ |

一、选择题:
1、A
[解析]:4.3~4.4,有1人,4.4~4.5有3人, 4.5~4.6有9人, 4.6~4.7有27人,
故后六组共有87人,每组分别有27、22、17、12、7、2人,
故a= 0.27, b= 78
2、B
[解析]:随机变量ξ的分布列为P(ξ=k)= ,k=1、2、3、4,c为常数
,k=1、2、3、4,c为常数
故P(ξ=1)+P(ξ=2)+ P(ξ=3)+P(ξ=4)=1
3、A
[解析]:如果随机变量ξ~B(n,p),则 Eξ= np,Dξ= np(1-p)又Eξ=7,Dξ=6
4、B
[解析]:因为15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为150×
5、D
[解析]:设随机变量ξ的概率分布为P(ξ=k)=pk?(1-p)1-k(k=0,1),则
P(ξ=0)=p,P(ξ=1)=1-p
Eξ=0×p +1×(1-p)= 1-p,
Dξ=[0-(1-p)]2×p+[1-(1-p)]2×(1-p)= p(1-p)
6、B
[解析]:Eξ=2,Dξ= 0.8
7、D
[解析]:成功次数ξ服从二项分布,每次试验成功的概率为1- =
= ,
,
8、C
9、D
10、A
二、填空题:
[解析]:随机变量ξ的分布列为P(ξ=k)= (k=0,1,2,…,10)
(k=0,1,2,…,10)
12、1.2
[解析]:设含红球个数为ξ,则ξ的分布列为:
ξ
0
1
2
P
0.1
0.6
0.3
∴Eξ=1.2
13、144
14、4760
[解析]:该公司一年后估计可获收益的期望是
三、解答题:
0
1
2
P
乙的技术水平较高
ξ=3,表明李明在第一、二次考试未通过,第三次通过了,故
ξ=4,表明李明第一、二、三次考试都未通过,故
∴李明实际参加考试次数ξ的分布列为
ξ
1
2
3
4
P
0.6
0.28
0.096
0.024
∴ξ的期望Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544.
李明在一年内领到驾照的概率为
1-(1-0.6)(1-0.7)(1-0.8)(1-0.9)=0.9976.
18、解:(I)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3. 由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,
P(A3)=0.6.
客人游览的景点数的可能取值为0,1,2,3. 相应地,客人没有游览的景点数的可能取值为3,2,1,0,所以 的可能取值为1,3.
的可能取值为1,3.
=2×0.4×0.5×0.6=0.24,
本资料来源于《七彩教育网》http://www.7caiedu.cn
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com