
17. 解:
(1)由
解:
(1)由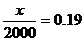 ,解得
,解得 ,
,
(2)初三年级人数为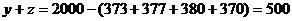 ,
,
设应在初三年级抽取m人,则 ,解得m=12.
,解得m=12.
答: 应在初三年级抽取12名.
(3)设初三年级女生比男生多的事件为 ,初三年级女生和男生数记为数对
,初三年级女生和男生数记为数对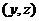 ,
,
由(2)知 ,则基本事件总数有:
,则基本事件总数有:

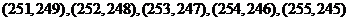 共11个,
共11个,
而事件 包含的基本事件有:
包含的基本事件有:
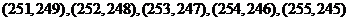 共5个,
共5个,
∴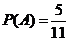
16、解:(Ⅰ)总体平均数为 .
.
(Ⅱ)设 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
从总体中抽取2个个体全部可能的基本结果有: ,
,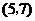 ,
,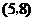 ,
,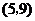 ,
, ,
, ,
,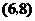 ,
,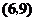 ,
, ,
,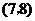 ,
,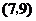 ,
, ,
,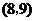 ,
,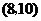 ,
,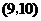 .共15个基本结果.
.共15个基本结果.
事件 包括的基本结果有:
包括的基本结果有: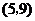 ,
, ,
,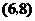 ,
,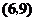 ,
, ,
,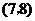 ,
,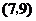 .共有7个基本结果.所以所求的概率为
.共有7个基本结果.所以所求的概率为 .
.
15.解:记“甲射击一次,命中7环以下”为事件 ,“甲射击一次,命中7环”为事件
,“甲射击一次,命中7环”为事件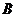 ,由于在一次射击中,
,由于在一次射击中, 与
与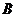 不可能同时发生,故
不可能同时发生,故 与
与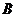 是互斥事件,
是互斥事件,
(1)“甲射击一次,命中不足8环”的事件为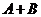 ,
,
由互斥事件的概率加法公式, .
.
答:甲射击一次,命中不足8环的概率是0.22.
(2) 记“甲射击一次,命中8环”为事件 ,“甲射击一次,命中9环(含9环)以上”为事件
,“甲射击一次,命中9环(含9环)以上”为事件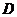 ,则“甲射击一次,至少命中7环”的事件为
,则“甲射击一次,至少命中7环”的事件为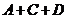 ,
,
∴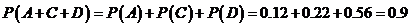 .
.
答:甲射击一次,至少命中7环的概率为0.9.
10. 
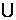
 11.
11.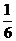 .
12.
.
12. . 13.
. 13. . 14.
. 14. .
.
1. 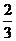 2.
2. 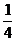 3.
3. 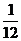 4.
4. 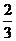 5.
5.  ,
, 6.
6. 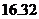 7.
7.  8.
8.  9.
9. 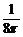
17.概率试题1
20.设有关于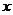 的一元二次方程
的一元二次方程 .
.
(Ⅰ)若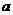 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若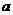 是从区间
是从区间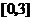 任取的一个数,
任取的一个数, 是从区间
是从区间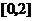 任取的一个数, 求上述方程有实根的概率.
任取的一个数, 求上述方程有实根的概率.
19.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为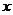 ,第二次出现的点数为
,第二次出现的点数为 .
.
(1)求事件“ ”的概率;
”的概率;
(2)求事件“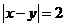 ”的概率.
”的概率.
18.现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语,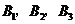 通晓俄语,
通晓俄语,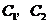 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求 被选中的概率 (Ⅱ)求
被选中的概率 (Ⅱ)求 和
和 不全被选中的概率.
不全被选中的概率.
17. 某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19
.
某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19
.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生, 问应在初三年级抽取多少名?
(3)已知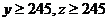 ,求初三年级中女生比男生多的概率.
,求初三年级中女生比男生多的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com