
8. 垂直于直线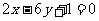 且与曲线
且与曲线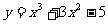 相切的直线方程是 。
相切的直线方程是 。
7. 平行于直线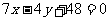 且与曲线
且与曲线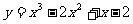 相切的直线方程是 。
相切的直线方程是 。
6. 曲线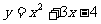 在点
在点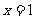 处的切线与
处的切线与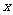 轴,
轴,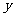 轴的交点分别是 与 。
轴的交点分别是 与 。
5. 已知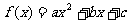 ,满足
,满足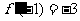 ,
,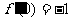 ,
,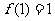 ,则
,则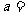 ,
,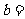 ,
,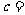 。
。
4. 已知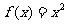 ,若
,若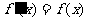 ,则
,则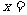 。
。
3. 某物体运动规律是 ,则在
,则在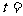 时的瞬时速度为0。
时的瞬时速度为0。
2. 与直线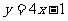 平行的曲线
平行的曲线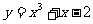 的切线方程是( )
的切线方程是( )
A. 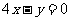 B.
B. 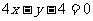
C. 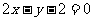 D.
D.
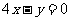 或
或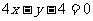
1. 抛物线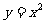 在点
在点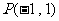 处的切线的倾斜角是( )
处的切线的倾斜角是( )
A. 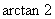 B.
B. 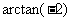 C.
C. 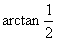 D.
D. 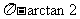
4. 导函数的概念
如果函数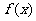 在开区间
在开区间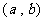 内每一点都可导,就说
内每一点都可导,就说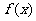 在
在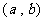 内可导,这时,对于开区间
内可导,这时,对于开区间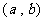 内每个确定的值
内每个确定的值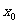 都对应一个确定的导数
都对应一个确定的导数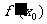 ,这就在
,这就在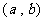 内构成一个新的函数,此函数就称为
内构成一个新的函数,此函数就称为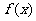 在
在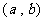 内的导函数,记作
内的导函数,记作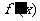 或
或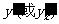 ,即
,即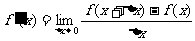
而当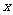 取定某一数值
取定某一数值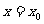 时的导数是上述导函数的一个函数值。
时的导数是上述导函数的一个函数值。
导数与导函数概念不同,导数是在一点处的导数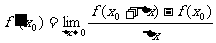 ,导函数是某一区间
,导函数是某一区间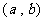 内的导数,对
内的导数,对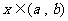
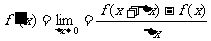
导函数是以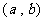 内任一点
内任一点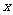 为自变量,以
为自变量,以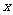 处的导数值为函数值的函数关系,导函数反映的是一般规律,而
处的导数值为函数值的函数关系,导函数反映的是一般规律,而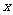 等于某一数值时的导数是此规律中的特殊性。
等于某一数值时的导数是此规律中的特殊性。
[典型例题]
[例1] 已知函数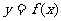 在
在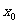 处存在导数
处存在导数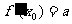 ,求
,求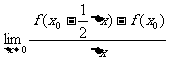 。
。
解:上式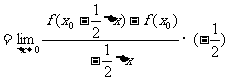
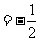
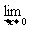
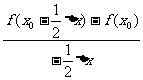
令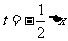 ,当
,当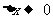 时,
时,
上式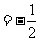
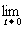
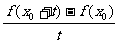
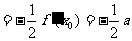
[例2] 已知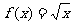 ,求导函数
,求导函数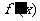
解: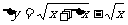
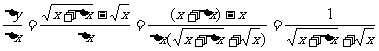
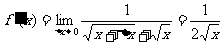
注:利用定义求导数的步骤
(1)求函数增量
(2)求平均变化率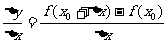
(3)取极限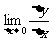
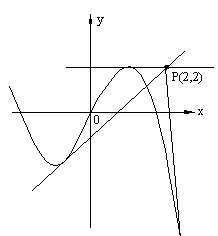
[例3] 已知曲线C: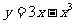 及点
及点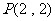 ,则过点P可向C引切线条数为( )
,则过点P可向C引切线条数为( )
A. 0 B. 1 C. 2 D. 3
解:设切点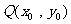 则切线
则切线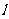 的方程为:
的方程为: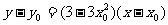
即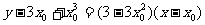

由点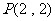 在直线
在直线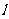 上,故
上,故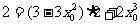
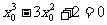
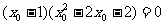
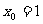 或
或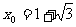 或
或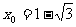
所以过点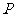 向C可引三条切线
向C可引三条切线
[模拟试题]
3. 导数的物理意义
函数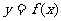 在
在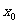 的导数是函数在该点处平均变化率的极限,即瞬时变化率,若函数
的导数是函数在该点处平均变化率的极限,即瞬时变化率,若函数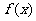 表示运动路程,则
表示运动路程,则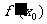 表示在
表示在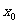 时刻的瞬时速度。
时刻的瞬时速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com