
2.含有三个实数的集合可表示为{a,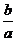 ,1},也可表示为{a2, a+b,0},则a2006+b2006
,1},也可表示为{a2, a+b,0},则a2006+b2006
的值为 ( )
A.0 B.1 C.-1 D.±1
1.若A、B、C为三个集合,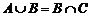 ,则一定有 ( )
,则一定有 ( )
A. B.
B. C.
C.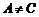 D.
D.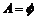
22.(14分)设函数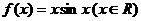 .
.
(Ⅰ)证明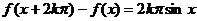 ,其中为k为整数;
,其中为k为整数;
(Ⅱ)设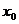 为
为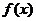 的一个极值点,证明
的一个极值点,证明 ;
;
(Ⅲ)设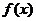 在(0,+∞)内的全部极值点按从小到大的顺序排列
在(0,+∞)内的全部极值点按从小到大的顺序排列 ,证明
,证明
21.(12分)已知函数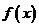 在R上有定义,对任何实数
在R上有定义,对任何实数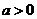 和任何实数
和任何实数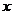 ,都有
,都有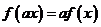
(Ⅰ)证明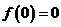 ;
;
(Ⅱ)证明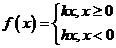 其中
其中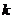 和
和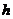 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的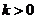 时,设
时,设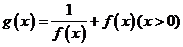 ,讨论
,讨论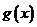 在
在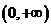 内的单调性并求极值。
内的单调性并求极值。
20.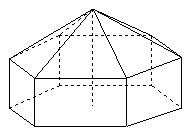 (12分)请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心
(12分)请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心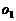 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
19.(12分)(理)抛物线y=ax2+bx在第一象限内与直线x+y=4相切.此抛物线与x轴所围成的图形的面积记为S.求使S达到最大值的a、b值,并求Smax.
(文)已知二次函数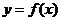 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为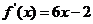 ,数列
,数列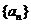 的前n项和为
的前n项和为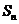 ,点
,点 均在函数
均在函数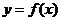 的图像上。
的图像上。
(Ⅰ)求数列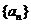 的通项公式;
的通项公式;
(Ⅱ)设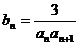 ,
,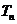 是数列
是数列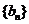 的前n项和,求使得
的前n项和,求使得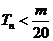 对所有
对所有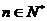 都成立的最小正整数m;
都成立的最小正整数m;
18. (12分)(理)已知复数
(12分)(理)已知复数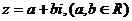
满足,复平面内有RtΔABC,其中∠BAC=90°,
点A、B、C分别对应复数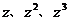 ,如图
,如图
所示,求z的值。
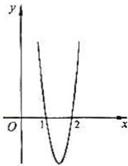 (文)已知函数
(文)已知函数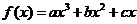 在点
在点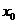 处取得极大值5,其导函数
处取得极大值5,其导函数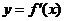
的图象经过点(1,0),(2,0),如图所示,求:
(Ⅰ)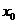 的值;
的值;
(Ⅱ)a,b,c 的值.
17.(12分)(理)求同时满足下列条件的所有的复数z, ①z+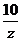 ∈R, 且1<z+
∈R, 且1<z+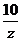 ≤6, ②z的实部和虚部都是整数。
≤6, ②z的实部和虚部都是整数。
(文)统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=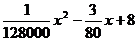 (0<x≤120).已知甲、乙两地相距100千米。
(0<x≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
16.(理)若非零复数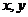 满足
满足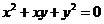 ,则
,则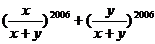 的值是
.
的值是
.
(文)等边三角形的高为8cm时, 面积对高的变化率为 .
15.曲线y=x3在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为_ _.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com