
18.解:∵Sn=1+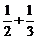 +…+
+…+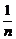 (n∈N*)
(n∈N*)
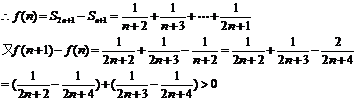
∴f(n+1)>f(n)
∴f(n)是关于n的增函数
∴f(n) min=f(2)=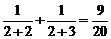
∴要使一切大于1的自然数n,不等式
f(n)>[logm(m-1)]2-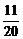 [log(m-1)m]2恒成立
[log(m-1)m]2恒成立
只要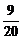 >[logm(m-1)]2-
>[logm(m-1)]2-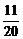 [log(m-1)m]2成立即可
[log(m-1)m]2成立即可
由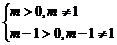 得m>1且m≠2
得m>1且m≠2
此时设[logm(m-1)]2=t 则t>0
于是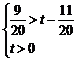
解得0<t<1
由此得0<[logm(m-1)]2<1
解得m>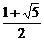 且m≠2。
且m≠2。
17.分析:由于{b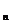 }和{c
}和{c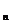 }中的项都和{a
}中的项都和{a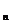 }中的项有关,{a
}中的项有关,{a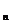 }中又有S
}中又有S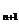 =4a
=4a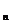 +2,可由S
+2,可由S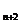 -S
-S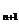 作切入点探索解题的途径.
作切入点探索解题的途径.
解析:(Ⅰ)由已知得,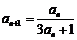 ,
,
∴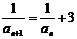 ,即
,即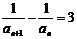
∴数列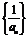 是首项
是首项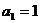 ,公差
,公差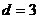 的等差数列.
的等差数列.
∴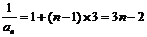 ,
,
故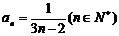
(Ⅱ) ∵
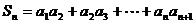
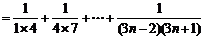
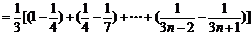
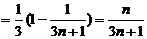 。
。
13.周长之和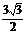 πa,面积之和
πa,面积之和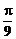 a2;14.1;15.-2;16.7;
a2;14.1;15.-2;16.7;
1.A;2.C;3.A;4.B;5.A;6.D;7.B;8.A;9.B;10.C;11.D;12.A;
22.(14分)已知数列{xn}的各项为不等于1的正数,其前n项和为Sn,点Pn的坐标为(xn,Sn),若所有这样的点Pn(n=1,2,…)都在斜率为k的同一直线(常数k≠0,1)上.
(Ⅰ)求证:数列{xn}是等比数列;
(Ⅱ)设yn=log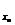 (2a2-3a+1)满足ys=
(2a2-3a+1)满足ys=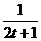 ,yt=
,yt= (s,t∈N,且s≠t)共中a为常数,
(s,t∈N,且s≠t)共中a为常数,
且1<a<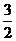 ,试判断,是否存在自然数M,使当n>M时,xn>1恒成立?若存在,求出相应的M;若不存在,请说明理由.
,试判断,是否存在自然数M,使当n>M时,xn>1恒成立?若存在,求出相应的M;若不存在,请说明理由.
考答案(5)
21.(12分)设数列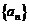 的前
的前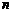 项和为
项和为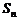 ,已知
,已知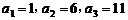 ,且
,且
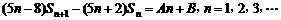 ,
,
其中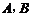 为常数.
为常数.
(Ⅰ)求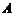 与
与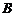 的值;
的值;
(Ⅱ)证明:数列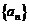 为等差数列;
为等差数列;
(Ⅲ)证明:不等式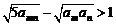 对任何正整数
对任何正整数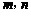 都成立.
都成立.
20.(12分)设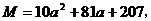
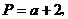
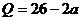 ,若将
,若将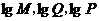 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列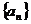 的前三项.
的前三项.
(Ⅰ)求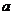 的值及
的值及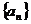 的通项公式;
的通项公式;
(Ⅱ)记函数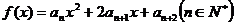 的图象在
的图象在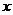 轴上截得的线段长为
轴上截得的线段长为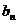 ,设
,设 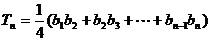 ,求
,求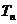
19.(12分)已知数列
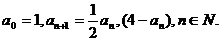
(Ⅰ)证明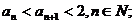 (Ⅱ)求数列
(Ⅱ)求数列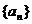 的通项公式an.
的通项公式an.
18.(12分)已知Sn=1+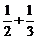 +…+
+…+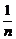 ,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-
,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-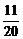 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.
17.(12分)已知函数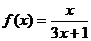 ,数列
,数列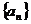 满足
满足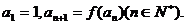
(Ⅰ)求数列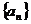 的通项公式;
的通项公式;
(Ⅱ)记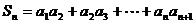 ,求
,求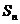 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com