
5.f(x)=kax-a-x(a>0且a≠1)既是奇函数,又是增函数,那么g(x)=loga(x+k)的图象是 ( )
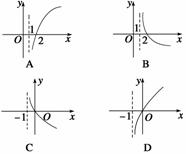
?
答案?D
4.(2009·宜昌调研)函数y=log (x2-3x+2)的递增区间是
(
)
(x2-3x+2)的递增区间是
(
)
?A.(-∞,1)? B.(2,+∞)
?C.(-∞,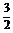 )?
D.(
)?
D.(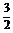 ,+∞)
,+∞)
答案?A?
3.已知点(m,n)在函数f(x)=ax的图象上,则下列哪个点一定在函数g(x)=-logax (a>0,a≠1)的图象上 ( )
?A.(n,m) B.(n,-m)
?C.(m,-n) D.(-m,n)
答案?B?
2.设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为 ,则a等于
( )
,则a等于
( )
?A.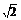 B.2
C.2
B.2
C.2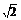 ?
D.4
?
D.4
答案?D?
1.若函数y=loga(x+b) (a>0,且a≠1)的图象过两点(-1,0)和(0,1),则 ( )
A.a=2,b=2
B.a=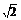 ,b=2
,b=2
C.a=2,b=1
?D.a=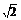 ,b=
,b=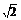
答案?A?
4.已知函数f(x)=log2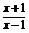 +log2(x-1)+log2(p-x).
+log2(x-1)+log2(p-x).
(1)求f(x)的定义域;
(2)求f(x)的值域.
解 (1)f(x)有意义时,有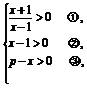
由①、②得x>1,由③得x<p,因为函数的定义域为非空数集,故p>1,f(x)的定义域是(1,p).
(2)f(x)=log2[(x+1)(p-x)]
=log2[-(x-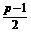 )2+
)2+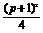 ] (1<x<p),
] (1<x<p),
①当1<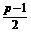 <p,即p>3时,
<p,即p>3时,
0<-(x-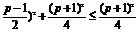 ,
,
∴log2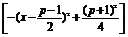 ≤2log2(p+1)-2.
≤2log2(p+1)-2.
②当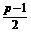 ≤1,即1<p≤3时,
≤1,即1<p≤3时,
∵0<-(x-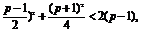
∴log2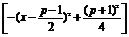 <1+log2(p-1).
<1+log2(p-1).
综合①②可知:
当p>3时,f(x)的值域是(-∞,2log2(p+1)-2];
当1<p≤3时,函数f(x)的值域是(-∞,1+log2(p-1)).

3.已知函数f(x)=log2(x2-ax-a)在区间(-∞,?1-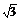 ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.
解 令g(x)=x2-ax-a,
则g(x)=(x-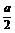 )2-a-
)2-a-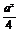 , 由以上知g(x)的图象关于直线x=
, 由以上知g(x)的图象关于直线x=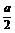 对称且此抛物线开口向上.
对称且此抛物线开口向上.
因为函数f(x)=log2g(x)的底数2>1,
在区间(-∞,1-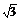 ]上是减函数,
]上是减函数,
所以g(x)=x2-ax-a在区间(-∞,1-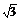 ]上也是单调减函数,且g(x)>0.
]上也是单调减函数,且g(x)>0.
∴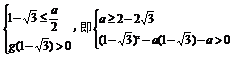
解得2-2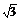 ≤a<2.
≤a<2.
故a的取值范围是{a|2-2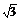 ≤a<2}.
≤a<2}.
2.已知0<a<1,b>1,ab>1,则loga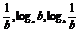 的大小关系是
( )
的大小关系是
( )
A.loga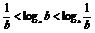 B.
B.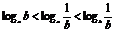
C.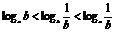 D.
D.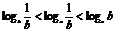
答案 C
1.化简求值.
(1)log2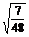 +log212-
+log212- log242-1;
log242-1;
(2)(lg2)2+lg2·lg50+lg25;
(3)(log32+log92)·(log43+log83).
解 (1)原式=log2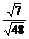 +log212-log2
+log212-log2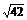 -log22
-log22
=log2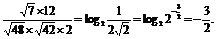
(2)原式=lg2(lg2+lg50)+lg25=2lg2+lg25=lg100=2.
(3)原式=(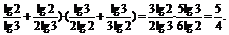
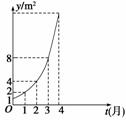
5.如图所示的是某池塘中的浮萍蔓延的面积y (m2)与时间t(月)的关系:y=at,有以下叙述:
①这个指数函数的底数为2;②第5个月时,浮萍面积就会超过30 m2;?③浮萍从4 m2蔓延到12 m2需要经过1.5个月;④浮萍每月增加的面积都相等;⑤若浮萍蔓延到2 m2、3 m2、6 m2所经过的时间分别为t1、t2、t3,则t1+t2=t3.
其中正确的是 ( )
 A.①②
B.①②③④
A.①②
B.①②③④
C.②③④⑤ ? D.①②⑤
答案?D?

例1 计算:(1)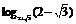
(2)2(lg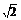 )2+lg
)2+lg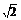 ·lg5+
·lg5+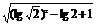 ;
;
(3) lg
lg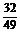 -
-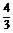 lg
lg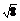 +lg
+lg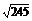 .
.
解 (1)方法一 利用对数定义求值
设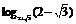 =x, 则(2+
=x, 则(2+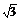 )x=2-
)x=2-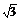 =
=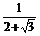 =(2+
=(2+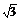 )-1,∴x=-1.
)-1,∴x=-1.
方法二 利用对数的运算性质求解
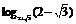 =
=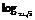
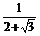 =
=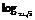 (2+
(2+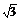 )-1=-1.
)-1=-1.
(2)原式=lg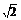 (2lg
(2lg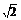 +lg5)+
+lg5)+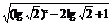 =lg
=lg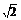 (lg2+lg5)+|lg
(lg2+lg5)+|lg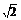 -1|
-1|
=lg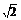 +(1-lg
+(1-lg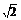 )=1.
)=1.
(3)原式= (lg32-lg49)-
(lg32-lg49)-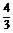 lg8
lg8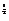 +
+ lg245
lg245
= (5lg2-2lg7)-
(5lg2-2lg7)-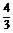 ×
×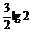 +
+ (2lg7+lg5)
(2lg7+lg5)
=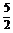 lg2-lg7-2lg2+lg7+
lg2-lg7-2lg2+lg7+ lg5=
lg5= lg2+
lg2+ lg5
lg5
= lg(2×5)=
lg(2×5)=  lg10=
lg10= .?
.?
例2 比较下列各组数的大小.
(1)log3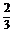 与log5
与log5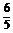 ;
;
(2)log1.10.7与log1.20.7;
(3)已知log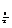 b<log
b<log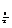 a<log
a<log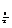 c,比较2b,2a,2c的大小关系.
c,比较2b,2a,2c的大小关系.
解 (1)∵log3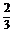 <log31=0,
<log31=0,
而log5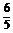 >log51=0,∴log3
>log51=0,∴log3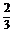 <log5
<log5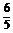 .
.
(2)方法一 ∵0<0.7<1,1.1<1.2,
∴0>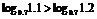 ,
,
∴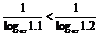 ,
,
即由换底公式可得log1.10.7<log1.20.7.
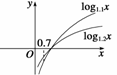 方法二 作出y=log1.1x与y=log1.2x的图象.
方法二 作出y=log1.1x与y=log1.2x的图象.
如图所示两图象与x=0.7相交可知log1.10.7<log1.20.7.
(3)∵y=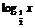 为减函数,且
为减函数,且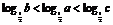 ,
,
∴b>a>c,而y=2x是增函数,∴2b>2a>2c.
例3 (12分)已知函数f(x)=logax(a>0,a≠1),如果对于任意x∈[3,+∞)都有|f(x)|≥1成立,试求a的取值范围.
解 当a>1时,对于任意x∈[3,+∞),都有f(x)>0.
所以,|f(x)|=f(x),而f(x)=logax在[3,+∞)上为增函数,
∴对于任意x∈[3,+∞),有f(x)≥loga3. 4分
因此,要使|f(x)|≥1对于任意x∈[3,+∞)都成立.
只要loga3≥1=logaa即可,∴1<a≤3. 6分
当0<a<1时,对于x∈[3,+∞),有f(x)<0,
∴|f(x)|=-f(x). 8分
∵f(x)=logax在[3,+∞)上为减函数,
∴-f(x)在[3,+∞)上为增函数.
∴对于任意x∈[3,+∞)都有
|f(x)|=-f(x)≥-loga3. 10分
因此,要使|f(x)|≥1对于任意x∈[3,+∞)都成立,
只要-loga3≥1成立即可,
∴loga3≤-1=loga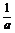 ,即
,即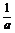 ≤3,∴
≤3,∴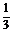 ≤a<1.
≤a<1.
综上,使|f(x)|≥1对任意x∈[3,+∞)都成立的a的取值范围是:(1,3]∪[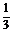 ,1).
12分
,1).
12分
例4 已知过原点O的一条直线与函数y=log8x的图象交于A、B两点,分别过A、B作y轴的平行线与函数y=log2x的图象交于C、D两点.
(1)证明:点C、D和原点O在同一直线上;
(2)当BC平行于x轴时,求点A的坐标.
(1)证明 设点A、B的横坐标分别为x1、x2,
由题设知x1>1,x2>1,则点A、B的纵坐标分别为log8x1、log8x2.
因为A、B在过点O的直线上,所以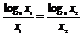
点C、D的坐标分别为(x1,log2x1)、(x2,log2x2),
由于log2x1=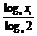 =3log8x1,log2x2=3log8x2,
=3log8x1,log2x2=3log8x2,
OC的斜率为k1=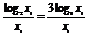 ,
,
OD的斜率为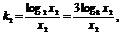 由此可知k1=k2,即O、C、D在同一直线上.
由此可知k1=k2,即O、C、D在同一直线上.
(2)解 由于BC平行于x轴,知log2x1=log8x2,即得log2x1=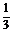 log2x2,x2=x31,
log2x2,x2=x31,
代入x2log8x1=x1log8x2,得x31log8x1=3x1log8x1,由于x1>1,知log8x1≠0,故x31=3x1,
又因x1>1,解得x1=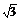 ,于是点A的坐标为(
,于是点A的坐标为(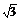 ,log8
,log8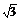 ).
).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com