
6.当x>0时,函数f(x)=(a2-1)x的值总大于1,则实数a的取值范围是 ( )
?A.1<|a|<2
B.|a|<1
?
C.|a|>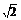 D.|a|<
D.|a|<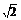
答案?C?
5.设函数f(x)=a-|x|(a>0,且a≠1),f(2)=4,则 ( ) A.f(-2)>f(-1) B.f(-1)>f(-2) C.f(1)>f(2)? D.f(-2)>f(2)
答案?A?
4.(2009·保定模拟)若f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是 ( )
?A.(-1,0) B.(-1,0)∪(0,1]? C.(0,1] D.(0,1)
答案?C?
3.若函数y=4x-3·2x+3的定义域为集合A,值域为[1,7],集合B=(-∞,0]∪[1,2],则集合A与集合B的关
系为 ( )
? A.A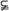 B? B.A=B C.B
B? B.A=B C.B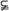 A
?D.无法确定
A
?D.无法确定
答案 B?
2.若a<0,则 ( )
?A.2a>( )a>(0.2)a
B.(0.2)a>(
)a>(0.2)a
B.(0.2)a>( )a>2a
)a>2a
?C.( )a>(0.2)a>2a D.2a>(0.2)a>(
)a>(0.2)a>2a D.2a>(0.2)a>( )a
)a
答案?B?
1.2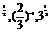 的大小顺序为
(
)
的大小顺序为
(
)
A.3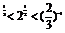 B.2
B.2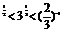
C.(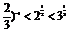 D.2
D.2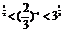
答案 B
4.已知定义在R上的奇函数f(x)有最小正周期2,且当x∈(0,1)时,f(x)=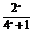 .
.
(1)求f(x)在[-1,1]上的解析式;
(2)证明:f(x)在(0,1)上是减函数.
(1)解 当x∈(-1,0)时,-x∈(0,1).
∵f(x)是奇函数,∴f(x)=-f(-x)=-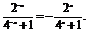 由f(0)=f(-0)=-f(0),且f(1)=-f(-1)=-f(-1+2)=-f(1),
由f(0)=f(-0)=-f(0),且f(1)=-f(-1)=-f(-1+2)=-f(1),
得f(0)=f(1)=f(-1)=0.∴在区间[-1,1]上,有 f(x)=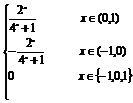
(2)证明 当x∈(0,1)时,f(x)=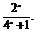
设0<x1<x2<1,
则f(x1)-f(x2)=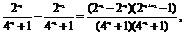
∵0<x1<x2<1,∴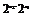 >0,2
>0,2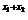 -1>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
-1>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在(0,1)上单调递减.

3.求下列函数的单调递增区间:
(1)y=(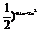 ;(2)y=2
;(2)y=2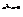 .
.
解 (1)函数的定义域为R.
令u=6+x-2x2,则y=(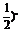 .
.
∵二次函数u=6+x-2x2的对称轴为x=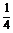 ,
,
在区间[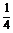 ,+∞)上,u=6+x-2x2是减函数,
,+∞)上,u=6+x-2x2是减函数,
又函数y=(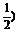 u是减函数,
u是减函数,
∴函数y=(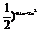 在[
在[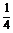 ,+∞)上是增函数.
,+∞)上是增函数.
故y=(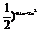 单调递增区间为[
单调递增区间为[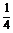 ,+∞).
,+∞).
(2)令u=x2-x-6,则y=2u,
∵二次函数u=x2-x-6的对称轴是x= ,
,
在区间[ ,+∞)上u=x2-x-6是增函数.
,+∞)上u=x2-x-6是增函数.
又函数y=2u为增函数,
∴函数y=2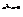 在区间[
在区间[ ,+∞)上是增函数.
,+∞)上是增函数.
故函数y=2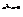 的单调递增区间是[
的单调递增区间是[ ,+∞).
,+∞).
2.已知实数a、b满足等式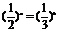 ,下列五个关系式:
,下列五个关系式:
①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.
其中不可能成立的关系式有 ( )
A.1个 ? B.2个 ?C.3个 ?D.4个
答案?B?
1.化简下列各式(其中各字母均为正数):
(1)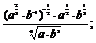
(2)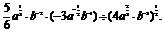
解 (1)原式=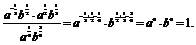
(2)原式=-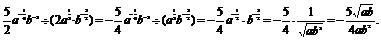
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com