
5.根据下面各个数列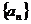 的首项和递推关系,求其通项公式
的首项和递推关系,求其通项公式
⑴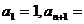
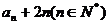
⑵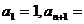
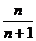
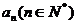
⑶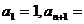
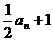
4.设在等比数列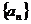 中,
中,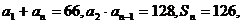 求
求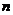 及
及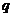
3.若数列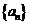 中,
中,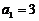 ,且
,且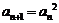
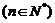 ,则数列的通项
,则数列的通项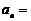 .
.
2.一个首项为正数的等差数列中,前3项的和等于前11项的和,当这个数列的前n项和最大时,n等于. ( )
A.5 B.6 C.7 D.8
1.设S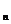 和T
和T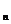 分别为两个等差数列的前n项和,若对任意n∈N,
分别为两个等差数列的前n项和,若对任意n∈N,

( )
A.4∶3 B.3∶2 C.7∶4 D.78∶71
例1.(08全国卷)设数列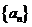 的前
的前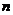 项和为
项和为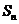 .已知
.已知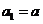 ,
,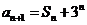 ,
,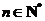 .
.
(Ⅰ)设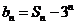 ,求数列
,求数列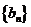 的通项公式;
的通项公式;
(Ⅱ)若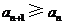 ,
,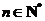 ,求
,求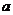 的取值范围.
的取值范围.
解:(Ⅰ)依题意,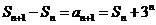 ,即
,即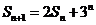 ,
,
由此得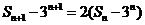 .
.
因此,所求通项公式为
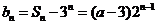 ,
,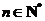 .①
.①
(Ⅱ)由①知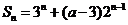 ,
,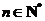 ,
,
于是,当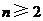 时,
时,
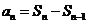
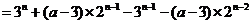
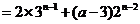 ,
,
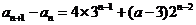
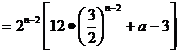 ,
,
当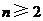 时,
时,
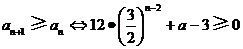
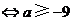 .
.
又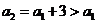 .
.
综上,所求的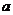 的取值范围是
的取值范围是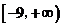 .
.
例2.(08山东高考题)将数列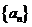 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
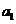
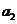
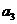
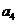
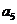
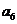
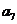
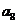
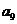
记表中的第一列数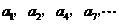 构成的数列为
构成的数列为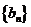 ,
,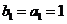 .
.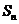 为数列
为数列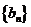 的前
的前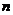 项和,且满足
项和,且满足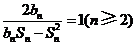 .
.
(Ⅰ)证明数列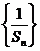 成等差数列,并求数列
成等差数列,并求数列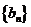 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数(Ⅰ)证明:由已知,当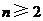 时,
时,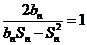 ,
,
又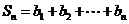 ,
,
所以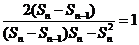 ,
,
即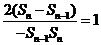 ,
,
所以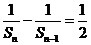 ,
,
又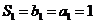 .
.
所以数列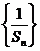 是首项为1,公差为
是首项为1,公差为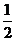 的等差数列.
的等差数列.
由上可知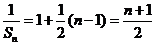 ,
,
即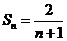 .
.
所以当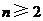 时,
时,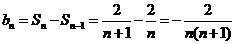 .
.
因此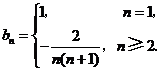
(Ⅱ)解:设上表中从第三行起,每行的公比都为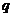 ,且
,且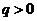 .
.
因为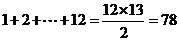 ,
,
所以表中第1行至第12行共含有数列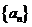 的前78项,
的前78项,
故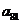 在表中第13行第三列,
在表中第13行第三列,
因此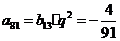 .
.
又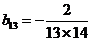 ,
,
所以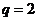 .
.
记表中第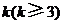 行所有项的和为
行所有项的和为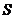 ,
,
则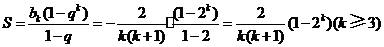 .当
.当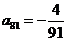 时,求上表中第
时,求上表中第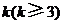 行所有项的和.
行所有项的和.
例3.(08宁夏)已知数列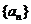 是一个等差数列,且
是一个等差数列,且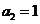 ,
,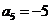 。
。
(1) 求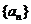 的通项
的通项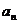 ;
;
(2) 求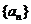 前n项和
前n项和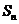 的最大值。
的最大值。
解:(Ⅰ)设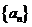 的公差为
的公差为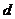 ,由已知条件,
,由已知条件,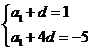 ,解出
,解出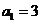 ,
,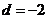 .
.
所以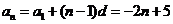 .
.
(Ⅱ)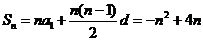
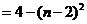 .
.
所以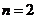 时,
时,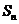 取到最大值
取到最大值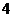 .
.
例4.(08广东)设数列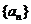 满足
满足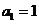 ,
,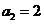 ,
,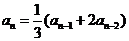
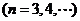 。数列
。数列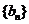 满足
满足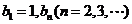 是非零整数,且对任意的正整数
是非零整数,且对任意的正整数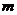 和自然数
和自然数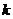 ,都有
,都有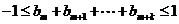 。
。
(1)求数列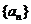 和
和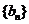 的通项公式;
的通项公式;
(2)记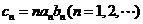 ,求数列
,求数列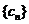 的前
的前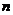 项和
项和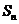 。
。
解:(1)由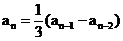 得
得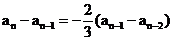 (n≥3)
(n≥3)
又a2-a1=1≠0,
∴数列{an+1-an}是首项为1公比为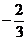 的等比数列,
的等比数列,
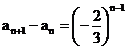
an=a1+(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)
=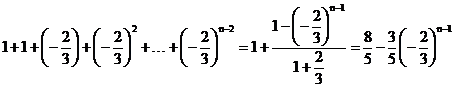 ,
,
由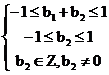 得b2=-1,由
得b2=-1,由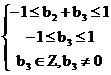 得b3=1,…
得b3=1,…
同理可得当n为偶数时,bn=-1;当n为奇数时,bn=1;
|
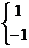
|
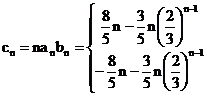
Sn=c1+c2+c3+c4+…+cn
当n为奇数时,
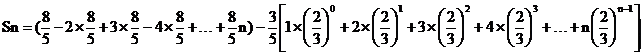
=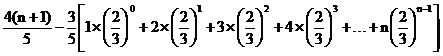
当n为偶数时
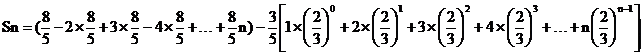
=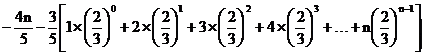
令Tn=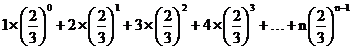 ……①
……①
①×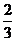 得:
得: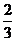 Tn=
Tn=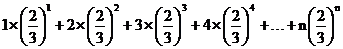 ……②
……②
①-②得: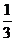 Tn =
Tn =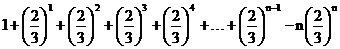
=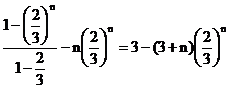 ∴Tn
=
∴Tn
=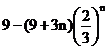
|
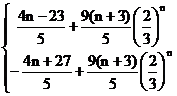
例5.设二次方程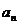 x
x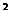 -
-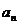 +1x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
+1x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
(1)试用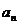 表示a
表示a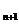 ;
;

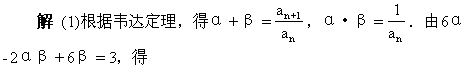
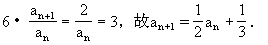
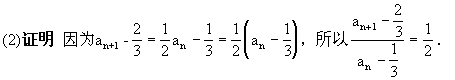
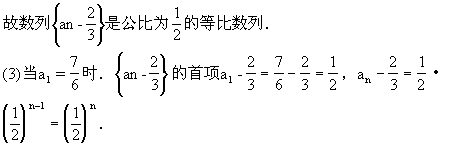
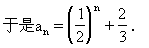
例6.数列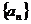 中,
中,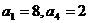 且满足
且满足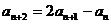
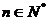
⑴求数列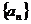 的通项公式;
的通项公式;
⑵设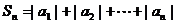 ,求
,求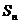 ;
;
⑶设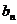 =
=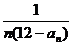
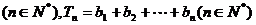 ,是否存在最大的整数
,是否存在最大的整数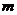 ,使得对任意
,使得对任意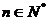 ,均有
,均有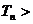
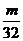 成立?若存在,求出
成立?若存在,求出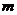 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(1)由题意,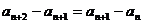 ,
,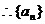 为等差数列,设公差为
为等差数列,设公差为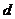 ,
,
由题意得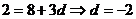 ,
,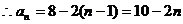 .
.
(2)若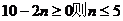 ,
,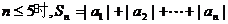
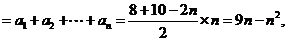
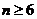 时,
时,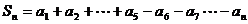
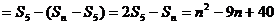

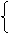 故
故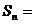
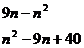
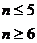
(3)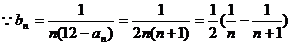
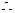
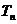
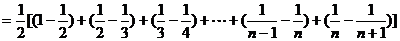
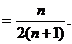
若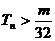 对任意
对任意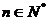 成立,即
成立,即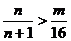 对任意
对任意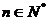 成立,
成立,
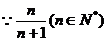 的最小值是
的最小值是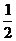 ,
,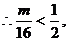
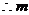 的最大整数值是7。
的最大整数值是7。
即存在最大整数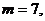 使对任意
使对任意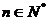 ,均有
,均有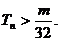 .w.w.k.s.5.u.c.o.
.w.w.k.s.5.u.c.o.
说明:本例复习数列通项,数列求和以及有关数列与不等式的综合问题。
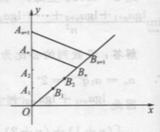 例7.如图,在y轴的正半轴上依次有点
例7.如图,在y轴的正半轴上依次有点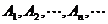 其中点
其中点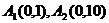 ,且
,且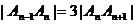
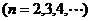 ,在射线
,在射线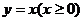 上依次有点
上依次有点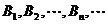 点
点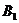 的坐标为(3,3),且
的坐标为(3,3),且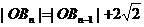
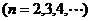
⑴用含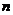 的式子表示
的式子表示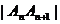 ;
;
⑵用含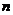 的式子表示
的式子表示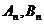 的坐标;
的坐标;
⑶求四边形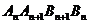 面积的最大值。
面积的最大值。
解:(1)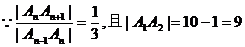 ,
,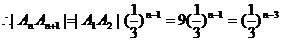
(2)由(1)得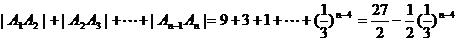
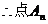 的坐标
的坐标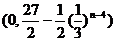 ,
,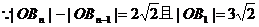
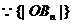 是以
是以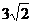 为首项,
为首项,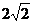 为公差的等差数列
为公差的等差数列
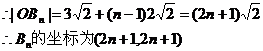
(3)连接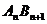 ,设四边形
,设四边形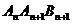
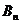 的面积为
的面积为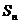 ,则
,则
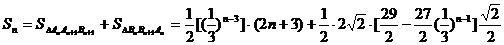
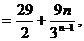
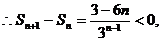
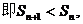
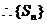 单调递减.
单调递减.
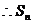 的最大值为
的最大值为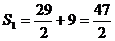 .
.
说明:本例为数列与几何的综合题。由题意知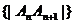 为等比,
为等比,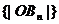 为等差,(3)利用函数单调性求最值。
为等差,(3)利用函数单调性求最值。
例8.设正数数列{a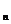 }为一等比数列,且a
}为一等比数列,且a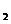 =4,a
=4,a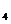 =16.
=16.
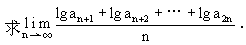
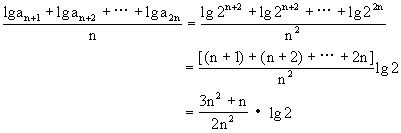
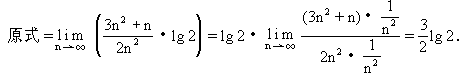
说明:本题涉及对数、数列、极限的综合题,主要考查等比数列的定义及通项公式,等差数列前n项和公式,对数计算,求数列极限等基础知识,以及综合运用数学知识的能力.
8.通过解题后的反思,找准自己的问题,总结成功的经验,吸取失败的教训,增强解综合题的信心和勇气,提高分析问题和解决问题的能力.
数列是高中数学的重要内容,又是学习高等数学的基础,所以在高考中占有重要的地位。高考对本章的考查比较全面,等差数列,等比数列的考查每年都不会遗漏。解答题多为中等以上难度的试题,突出考查考生的思维能力,解决问题的能力,试题大多有较好的区分度。有关数列的试题经常是综合题,经常把数列知识和指数函数、对数函数和不等式的知识综合起来,试题也常把等差数列、等比数列,数学归纳法综合在一起。探索性问题是高考的热点,常在数列解答题中出现。本章中还蕴含着丰富的数学思想,在主观题中着重考查函数与方程、转化与化归、分类讨论等重要思想,以及配方法、换元法、待定系数法等基本数学方法。应用问题考查的重点是现实客观事物的数学化,常需构造数列模型,将现实问题转化为数学问题来解决。
7.解综合题的成败在于审清题目,弄懂来龙去脉,透过给定信息的表象,抓住问题的本质,揭示问题的内在联系和隐含条件,明确解题方向,形成解题策略.
6.数列的综合题形式多样,解题思路灵活,但万变不离其宗,就是离不开数列的概念和性质,离不开数学思想方法,只要能把握这两方面,就会迅速打通解题思路.
5.注意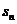 与
与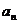 之间关系的转化。如:
之间关系的转化。如:
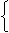
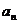 =
= 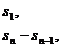
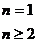 ,
, 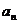 =
=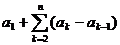 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com