
26.(本题共10分)
某私立中学准备招聘教职员工60名,所有员工的月工资情况如下:
|
员工 |
管理人员 |
教学人员 |
|||||
|
人员结构 |
校长 |
副校长 |
部处主任 |
教研组长 |
高级教师 |
中级教师 |
初级教师 |
|
员工人数/人 |
1 |
2 |
4 |
10 |
|
|
3 |
|
每人月工资/元 |
20000 |
17000 |
2500 |
2300 |
2200 |
2000 |
900 |
请根据上表提供的信息,回答下列问题:
(1)如果学校准备招聘“高级教师”和“中级教师”共40名(其他员工人数不变),其中高级教师至少要招聘13人,而且学校对高级、中级教师的月支付工资不超过83000元,按学校要求,对高级、中级教师有几种招聘方案?
(2) (1)中的哪种方案对学校所支付的月工资最少?并说明理由.
(3)在学校所支付的月工资最少时,将上表补充完整,并求所有员工月工资的中位数和众数.
25.(本题共10分)
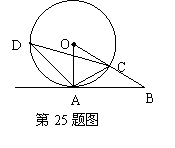
已知:如图,A是⊙O上一点,半径OC的延长线与过点A
的直线交于B点,OC=BC,AC=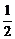 OB.
OB.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若D为⊙O上一点,∠ACD=45°,AD=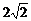 ,求扇形OAC的面积.
,求扇形OAC的面积.
24.(本题共10分)
张红和王伟为了争取到一张观看奥运知识竞赛的入场券,他们各自设计了一个方案:
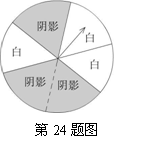
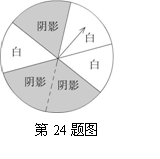 张红的方案是:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘)。
张红的方案是:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘)。
王伟的方案是:从一副扑克牌中取出方块1、2、3,将它们背
面朝上重新洗牌后,从中摸出一张,记录下牌面数字后放回,洗匀
后再摸出一张.若摸出两张牌面数字之和为奇数,则张红得到入场
劵;若摸出两张牌面数字之和为偶数,则王伟得到入场券.
(1)计算张红获得入场券的概率,并说明张红的方案是否公平?
(2)用树状图(或列表法)列举王伟设计方案的所有情况,计算王伟获得入场券的概率,并说明王
 伟的方案是否公平?
伟的方案是否公平?
23.(本题共10分)
 已知,如图,等腰梯形ABCD中,AD∥BC,AB=DC.
已知,如图,等腰梯形ABCD中,AD∥BC,AB=DC.
(1)试用直尺(不带刻度)和圆规在图中作出底边AD的中点E;
(不要求写作法,也不必说明理由,但要保留作图痕迹)。
(2) 连结EB、EC,求证:∠ABE=∠DCE.
22.(本题共8分)
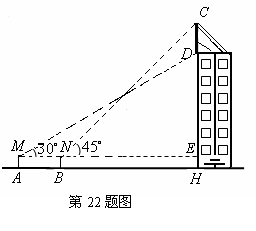 如图某幢大楼顶部有广告牌
如图某幢大楼顶部有广告牌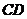 .张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为
.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为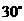 ;接着他向大楼前进14米站在点B处,测得广告牌顶端点C的仰角为
;接着他向大楼前进14米站在点B处,测得广告牌顶端点C的仰角为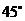 .(计算结果保留一位小数)
.(计算结果保留一位小数)
(1)求这幢大楼的高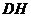 ;
;
(2)求这块广告牌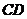 的高度.
的高度.





21.(本题共8分)
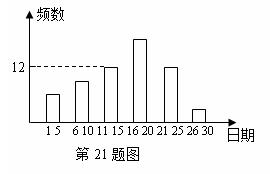 某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2∶3∶4∶6∶4∶1.请你回答:
某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2∶3∶4∶6∶4∶1.请你回答:
(1)本次活动共有
件作品参赛;上交作
品最多的组有作品
件;
(2)经评比,第四组和第六组分别有10件和2件
作品获奖,那么你认为这两组中哪个组获奖率
较高?为什么?

20.(本题共8分)
先化简分式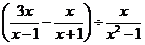 ,再从-1、0、1、2、3这五个数据中选一个合适的数作为x的值代入求值.
,再从-1、0、1、2、3这五个数据中选一个合适的数作为x的值代入求值.



19.(本题共8分)
(1)计算: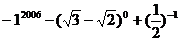 (2) 解方程:
(2) 解方程: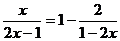




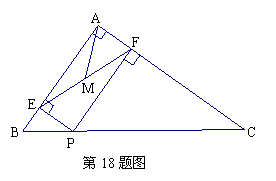
18.Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC
 于F,M为EF中点,则AM的最小值为
.
于F,M为EF中点,则AM的最小值为
.







|


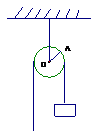
17.一个定滑轮起重装置如图所示,滑轮的半径是10cm,当重物上升20cm时,滑轮的一条
半径OA绕轴心按逆时针方向旋转的角度(假设绳索之间没有滑动,结果精确到1°)约
为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com