
6. (北京市十一学校2008届高三数学练习题)已知双曲线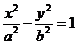 (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为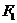 、
、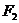 ,点A在双曲线第一象限的图象上,若△
,点A在双曲线第一象限的图象上,若△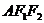 的面积为1,且
的面积为1,且
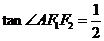 ,
,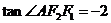 ,则双曲线方程为
( )
,则双曲线方程为
( )
A. 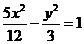 B.
B.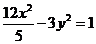 C.
C.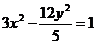 D.
D.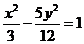
答案 B
5. (北京市朝阳区2008年高三数学一模)已知双曲线 的左、右焦点分别为
的左、右焦点分别为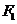 、
、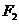 ,抛物线
,抛物线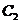 的顶点在原点,它的准线与双曲线
的顶点在原点,它的准线与双曲线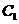 的左准线重合,若双曲线
的左准线重合,若双曲线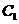 与抛物线
与抛物线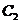 的交点
的交点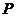 满足
满足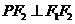 ,则双曲线
,则双曲线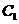 的离心率为( )
的离心率为( )
A. B. C. D.2
答案 B
4.(安徽省巢湖市2008届高三第二次教学质量检测)以椭圆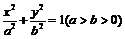 的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为
的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为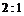 的两段弧,那么该椭圆的离心率等于
(
)
的两段弧,那么该椭圆的离心率等于
(
)
A.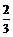 B.
B.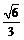 C.
C.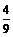 D.
D.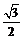
答案 B
3. (江西省五校2008届高三开学联考)从一块短轴长为2b的椭圆形玻璃镜中划出一块面积最
大的矩形,其面积的取值范围是[3b2,4b2],则这一椭圆离心率e的取值范围是 ( )
A.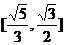 B.
B.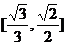 C.
C.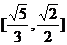 D.
D.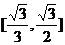
答案 A
2.(安徽省皖南八校2008届高三第一次联考)已知倾斜角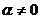 的直线
的直线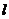 过椭圆
过椭圆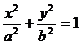
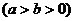 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则 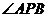 为
( )
为
( )
A.钝角 B.直角 C.锐角 D.都有可能
答案 C
1.(江苏省启东中学2008年高三综合测试四)设F1,F2是椭圆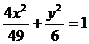 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且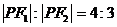 ,则
,则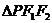 的面积为
( )
的面积为
( )
A.4 B.6
C.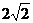 D.
D.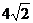
答案 B
19. (福建省龙岩市2009年普通高中毕业班单科质量检查)已知抛物线C: 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线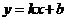 与抛物线C交于两点
与抛物线C交于两点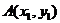 ,
,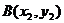 ,且
,且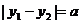 (
(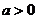 ,且
,且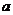 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于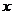 轴的直线交抛物线于点D,连结AD、 BD得到
轴的直线交抛物线于点D,连结AD、 BD得到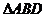 .
.
(1)求证: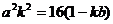 ;
;
(2)求证: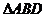 的面积为定值.
的面积为定值.
解 (1)依题意得: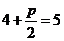 ,解得
,解得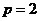 .
.
所以抛物线方程为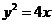 .
.
(2)由方程组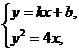 消去
消去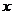 得:
得: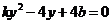 .(※)
.(※)
依题意可知: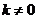 .
.
由已知得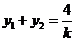 ,
,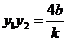 .
.
由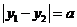 ,得
,得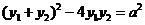 ,
,
即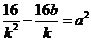 ,整理得
,整理得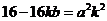 .
.
所以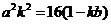 .
.
(Ⅲ)由(Ⅱ)知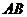 中点
中点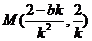 ,
,
所以点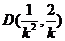 ,
,
依题意知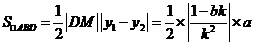 .
.
又因为方程(※)中判别式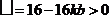 ,得
,得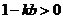 .
.
所以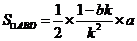 ,由(Ⅱ)可知
,由(Ⅱ)可知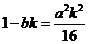 ,
,
所以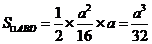 .
.
又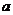 为常数,故
为常数,故 的面积为定值.
的面积为定值.
2007-2008年联考题
18.(2009年抚顺市普通高中应届毕业生高考模拟考试)设椭圆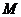 :
: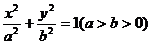 的离心率为
的离心率为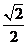 ,点
,点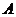 (
(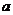 ,0),
,0),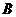 (0,
(0,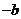 ),原点
),原点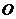 到直线
到直线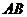 的距离为
的距离为 .
.
(Ⅰ)求椭圆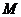 的方程;
的方程;
(Ⅱ)设点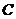 为(
为(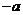 ,0),点
,0),点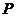 在椭圆
在椭圆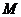 上(与
上(与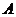 、
、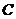 均不重合),点
均不重合),点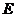 在直线
在直线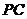 上,若直线
上,若直线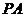 的方程为
的方程为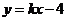 ,且
,且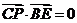 ,试求直线
,试求直线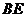 的方程.
的方程.
解 (Ⅰ)由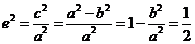 得
得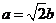
由点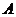 (
(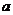 ,0),
,0),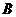 (0,
(0,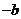 )知直线
)知直线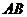 的方程为
的方程为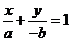 ,
,
于是可得直线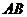 的方程为
的方程为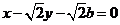
因此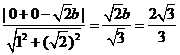 ,得
,得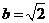 ,
,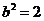 ,
,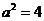 ,
,
所以椭圆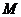 的方程为
的方程为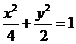
(Ⅱ)由(Ⅰ)知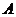 、
、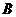 的坐标依次为(2,0)、
的坐标依次为(2,0)、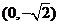 ,
,
因为直线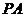 经过点
经过点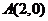 ,所以
,所以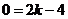 ,得
,得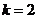 ,
,
即得直线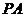 的方程为
的方程为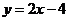
因为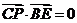 ,所以
,所以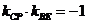 ,即
,即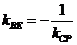
设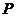 的坐标为
的坐标为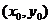 ,则
,则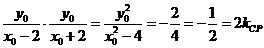
得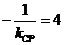 ,即直线
,即直线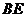 的斜率为4
的斜率为4
又点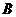 的坐标为
的坐标为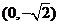 ,因此直线
,因此直线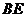 的方程为
的方程为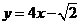
17. (2009届山东省实验中学高三年级第四次综合测试)直线y=kx+b与曲线
(2009届山东省实验中学高三年级第四次综合测试)直线y=kx+b与曲线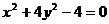 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值;
(3)当|AB|=2,S=1时,求直线AB的方程.
解 (1)曲线的方程可化为: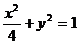 ,
,
∴此曲线为椭圆,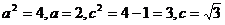 ,
,
∴此椭圆的离心率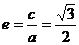 .
.
(2)设点A的坐标为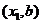 ,点B的坐标为
,点B的坐标为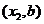 ,
,
由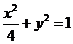 ,解得
,解得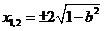 ,
,
所以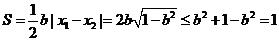
当且仅当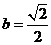 时,
S取到最大值1.
时,
S取到最大值1.
(3)由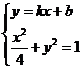 得
得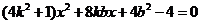 ,
,
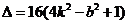 ①
①
|AB|=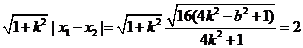 ②
②
又因为O到AB的距离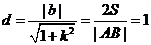 ,所以
,所以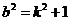 ③
③
③代入②并整理,得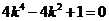
解得,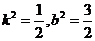 ,代入①式检验,△>0 ,
,代入①式检验,△>0 ,
故直线AB的方程是
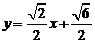 或
或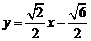 或
或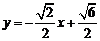 或
或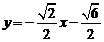 .
.
16.(东北区三省四市2009年第一次联合考试)过抛物线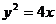 的焦点F的直线交抛物线于
的焦点F的直线交抛物线于
A、B两点,则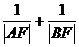 = 。
= 。
答案 1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com