
26. (江苏省启东中学高三综合测试四)已知以向量v=(1, 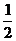 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 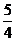 ),抛物线C:
),抛物线C: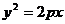 (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若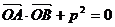 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
解 (Ⅰ)由题意可得直线l: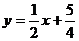 ①
①
过原点垂直于l的直线方程为 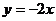 ②
②
解①②得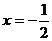 .
.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上.
∴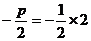 ,
,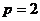
∴抛物线C的方程为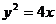 .
.
(Ⅱ)设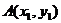 ,
,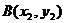 ,
,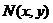 ,
,
由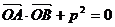 ,得
,得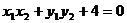 .
.
又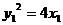 ,
,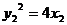 .
.
解得 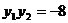 ③
③
直线ON: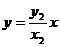 ,即
,即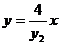 ④
④
由③、④及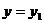 得,
得,
点N的轨迹方程为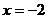
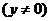 .
.
25.(湖北省八校高2008第二次联考)已知A,B是抛物线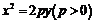 上的两个动点,
上的两个动点,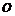 为坐标原点,非零向量
为坐标原点,非零向量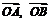 满足
满足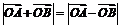 .
.
(Ⅰ)求证:直线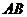 经过一定点;
经过一定点;
(Ⅱ)当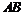 的中点到直线
的中点到直线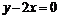 的距离的最小值为
的距离的最小值为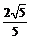 时,求
时,求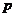 的值.
的值.
(1)证明 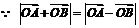 ,
, 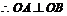 .设A,B两点的坐标为(
.设A,B两点的坐标为(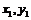 ),(
),(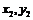 )
)
则 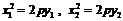 .
.
经过A,B两点的直线方程为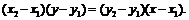
由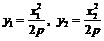 ,得
,得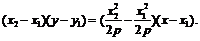
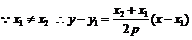 .
令
.
令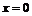 ,得
,得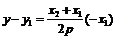 ,
, 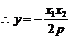 .
.
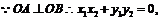 从而
从而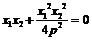 .
. 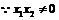 (否则,
(否则, 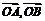 有一个为零向量),
有一个为零向量),
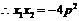 . 代入①,得
. 代入①,得 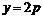 ,
,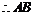 始终经过定点
始终经过定点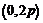 .
.
(2)解 设AB中点的坐标为(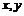 ),
),
则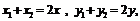
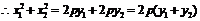 .
.
又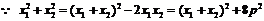 ,
, 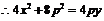 ,
,
即 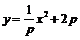 ①
①
AB的中点到直线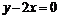 的距离
的距离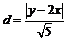 .
.
将①代入,得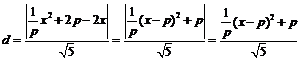 .
.
因为d的最小值为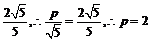 .
.
24.
(河南省开封市2008届高三年级第一次质量检)双曲线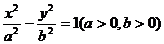 的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
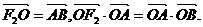
(1)求双曲线的离心率e;
(2)若此双曲线过C(2,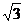 ),求双曲线的方程;
),求双曲线的方程;
(3)在(2)的条件下,D1、D2分别是双曲线的虚轴端点(D2在y轴正半轴上),过D1的直线l交双曲线M、N,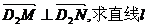 的方程。
的方程。
解(1)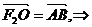 四边形F2 ABO是平行四边形
四边形F2 ABO是平行四边形
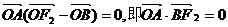
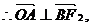
∴四边形F2 ABO是菱形.
∴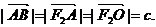
由双曲线定义得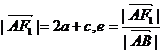
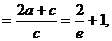
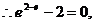
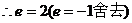
(2)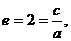
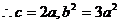 ,双曲线方程为
,双曲线方程为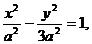
把点C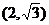 代入有
代入有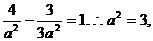
∴双曲线方程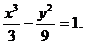
(3)D1(0,-3),D2(0,3),设l的方程为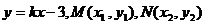
则由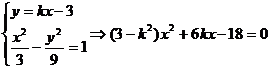
因l与与双曲线有两个交点,
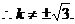
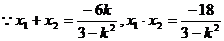
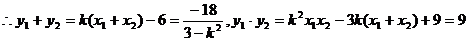
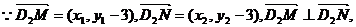
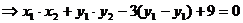
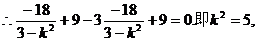
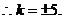 故所求直线l方程为
故所求直线l方程为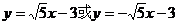 .
.
23.(2007北京四中模拟二)椭圆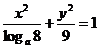 的离心率为
的离心率为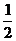 ,则a=________
,则a=________
答案 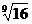
22.(2007届高三名校试题)A的坐标是(-2,0),B是圆F:(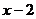 )
)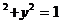 上的动点(F为圆心),线段AB的垂直平分线交直线BF于P,则动点P的轨迹方程为 。
上的动点(F为圆心),线段AB的垂直平分线交直线BF于P,则动点P的轨迹方程为 。
答案
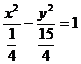
21.(2007届高三名校试题)椭圆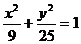 上的一点P到两焦点的距离的乘积为m,则
上的一点P到两焦点的距离的乘积为m,则
当m取最大值时,点P的坐标是 .
答案 (-3,0)或(3,0)
20. (湖北省黄冈市2007年秋季高三年级期末考试)已知点P是抛物线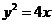 上的动点,点P在y轴上的射影是M,点A的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A的坐标是(4,a),则当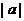
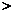 4时,
4时,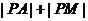 的最小值是
。
的最小值是
。
答案 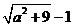
19. (福建省漳州一中2008年上期期末考试)双曲线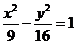 的两个焦点为
的两个焦点为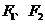 ,点
,点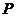 在该双曲线上,若
在该双曲线上,若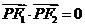 ,则点
,则点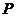 到
到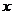 轴的距离为
.
轴的距离为
.
答案 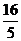
18. (福建省泉州一中高2008届第一次模拟检测)若双曲线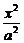 -
-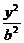 =1的渐近线与方程为
=1的渐近线与方程为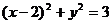 的圆相切,则此双曲线的离心率为
.
的圆相切,则此双曲线的离心率为
.
答案 2
17. (福建省南靖一中2008年第四次月考)过椭圆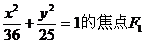 作直线交椭圆于A、B两点,F2是此椭圆的另一焦点,则
作直线交椭圆于A、B两点,F2是此椭圆的另一焦点,则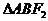 的周长为
.
的周长为
.
答案 24
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com